
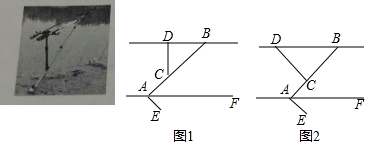
分析 (1)由平行得:∠DBC=∠CAG,根据等角的三角函数列式,求CG的长,距离为DG可求;
(2)由(1)的结论,根据∠HCB=∠CDB,cos∠HCB=cos∠CDB=$\frac{CH}{BC}=\frac{DH}{DC}$,设DH=2x,DC=3x,
由勾股定理列方程可得结论.
解答 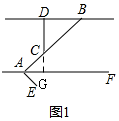 解:(1)如图1,延长DC交AF于G,
解:(1)如图1,延长DC交AF于G,
∵CD⊥BD,BD∥AF,
∴CD⊥AF,∠DBC=∠CAG,
sin∠DBC=sin∠CAG=$\frac{CD}{BC}=\frac{CG}{AC}$,
∴$\frac{40}{60}=\frac{CG}{30}$,
∴CG=20,
∴DG=40+20=60,
即钓鱼竿BD距地面的高度为60cm;
故答案为:60;
(2)如图2,过C作GH⊥BD,交BD于H,交AF于G,则GH⊥AF,
由(1)得:CH=40,BC=60,
∵∠BCD=90°,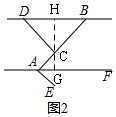
∴∠CDB+∠DBC=90°,
∵∠HCB+∠DBC=90°,
∴∠HCB=∠CDB,
cos∠HCB=cos∠CDB=$\frac{CH}{BC}=\frac{DH}{DC}$,
∴$\frac{40}{60}=\frac{DH}{DC}=\frac{2}{3}$,
设DH=2x,DC=3x,
由勾股定理得:(2x)2+402=(3x)2,
x=$±8\sqrt{5}$,
∵x>0,
∴x=8$\sqrt{5}$,
∴CD=3x=24$\sqrt{5}$,
答:支架CD的长度应该调节为24$\sqrt{5}$cm.
点评 本题是解直角三角形的应用问题,考查了三角函数、勾股定理、平行线的性质,熟练掌握三角函数的定义是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
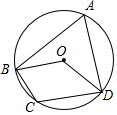 如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )
如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )| A. | π | B. | $\frac{3}{2}π$ | C. | 2π | D. | 3π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 重量(千克) 费用(元) | 0.5 | 1 | 3 | 4 | … |
| 甲公司 | 11 | 22 | 52 | 67 | … |
| 乙公司 | 11 | 19 | 51 | 67 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价x(元) | 60 | 70 | 80 | 90 | … |
| 销售量y(件) | 280 | 260 | 240 | 220 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com