
【题目】如图,以![]() 边为直径的⊙
边为直径的⊙![]() 经过点
经过点![]() ,
, ![]() 是⊙
是⊙![]() 上一点,连结
上一点,连结![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,
, ![]() .
.
(1)试判断![]() 与⊙
与⊙![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若点![]() 是弧
是弧![]() 的中点,已知
的中点,已知![]() ,求
,求![]() 的值.
的值.

【答案】(1)![]() 是⊙
是⊙![]() 的切线.证明见解析;(2)8.
的切线.证明见解析;(2)8.
【解析】试题分析:(1)连结OP,根据圆周角定理可得∠AOP=2∠ACP=120°,然后计算出∠PAD和∠D的度数,进而可得∠OPD=90°,从而证明PD是⊙O的切线;
(2)连结BC,首先求出∠CAB=∠ABC=∠APC=45°,然后可得AC长,再证明△CAE∽△CPA,进而可得![]() ,然后可得CECP的值.
,然后可得CECP的值.
试题解析:(1)如图, ![]() 是⊙
是⊙![]() 的切线.证明如下:
的切线.证明如下:
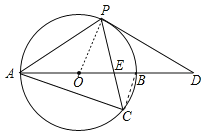
连结OP,
∵∠ACP=60°,
∴∠AOP=120°,
∵OA=OP,
∴∠OAP=∠OPA=30°,
∵PA=PD,
∴∠PAO=∠D=30°,
∴∠OPD=90°,
∴PD是⊙O的切线.
(2)连结BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
又∵C为弧AB的中点,
∴∠CAB=∠ABC=∠APC=45°,
∵AB=4,AC=ABsin45°=2![]() .
.
∵∠C=∠C,∠CAB=∠APC,
∴△CAE∽△CPA,
∴![]() ,
,
∴CPCE=CA2=(2![]() )2=8.
)2=8.


科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的图形W和点P,给出如下定义:F为图形W上任意一点,将P,F两点间距离的最小值记为m,最大值记为M,称M与m的差为点P到图形W的“差距离”,记作d(P,W),即d(P,W)=M-m,已知点A(2,1),B(-2,1)
(1)求d(O,AB);
(2)点C为直线y=1上的一个动点,当d(C,AB)=1时,点C的横坐标是 ;
(3)点D为函数y=x+b(-2≤x≤2)图象上的任意一点,当d(D,AB)≤2时,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科学考察队的一辆越野车需要穿越650千米的沙漠,但这辆车每次装满汽油最多只能行驶600千米,队长想出一个方法,在沙漠中设一个储油点![]() ,越野车装满油从起点
,越野车装满油从起点![]() 出发,到储油点
出发,到储油点![]() 时从车中取出部分油放进
时从车中取出部分油放进![]() 储油点,然后返回出发点
储油点,然后返回出发点![]() ,加满油后再开往
,加满油后再开往![]() ,到
,到![]() 储油点时取出储存的所有油放在车上,再到达终点.用队长想出的方法,这辆越野车穿越这片沙漠的最大行程是____________千米.
储油点时取出储存的所有油放在车上,再到达终点.用队长想出的方法,这辆越野车穿越这片沙漠的最大行程是____________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某司机在东西路上开车接送乘客,他早晨从A地出发,(去向东的方向正方向),到晚上送走最后一位客人为止,他一天行驶的的里程记录如下(单位:㎞)
+10 ,— 5, —15 ,+ 30 ,—20 ,—16 ,+ 14
(1) 若该车每百公里耗油 3 L ,则这车今天共耗油 多少升?
(2) 据记录的情况,你能否知道该车送完最后一个乘客是,他在A地的什么方向?距A地多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】泰兴出租车司机小李某天下午的营运全是在东西走向的国庆路上进行的,若规定向东为正,向西为负,这天下午的行车里程如下(单位:千米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:千米).
(单位:千米).
(1)将最后一名乘客送到目的地后,小李距下午出发地点的距离是多少千米?
(2)若出租车每行驶![]() 耗油
耗油![]() ,这天下午这辆出租车共消耗多少升汽油?
,这天下午这辆出租车共消耗多少升汽油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一列数:![]() ,
,![]() ,0,-22,-(+2),-(-4),请回答下列问题:
,0,-22,-(+2),-(-4),请回答下列问题:
(1)其中非负整数是_______________;(2)到原点距离相等的数是________________;
(3)画出数轴,并在数轴上表示这一列数,再用“<”连接起来.
查看答案和解析>>
科目:初中数学 来源: 题型:
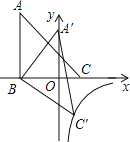
【题目】如图,△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y=![]() 的图象上,则k的值为__.
的图象上,则k的值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度![]() (单位:
(单位:![]() )与足球被踢出后经过的时间
)与足球被踢出后经过的时间![]() (单位:
(单位:![]() )之间的关系如下表:
)之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为![]() ;②足球飞行路线的对称轴是直线
;②足球飞行路线的对称轴是直线![]() ;③足球被踢出
;③足球被踢出![]() 时落地;④足球被踢出
时落地;④足球被踢出![]() 时,距离地面的高度是
时,距离地面的高度是![]() .
.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com