
【题目】已知关于x的一元二次方程x2=2(1﹣m)x﹣m2的两实数根为x1,x2
(1)求m的取值范围;
(2)设y=x1+x2,当y取得最小值时,求相应m的值,并求出最小值.
【答案】(1)、m≤![]() ;(2)、m=
;(2)、m=![]() 时,取得最小值1.
时,取得最小值1.
【解析】
试题分析:(1)、若一元二次方程有两不等根,则根的判别式△=b2﹣4ac≥0,建立关于m的不等式,可求出m的取值范围;(2)、根据根与系数的关系可得出x1+x2的表达式,进而可得出y、m的函数关系式,根据函数的性质及(1)题得出的自变量的取值范围,即可求出y的最小值及对应的m值.
试题解析:(1)、将原方程整理为x2+2(m﹣1)x+m2=0; ∵原方程有两个实数根,
∴△=[2(m﹣1)]2﹣4m2=﹣8m+4≥0,得m≤![]() ;
;
(2)、∵x1,x2为一元二次方程x2=2(1﹣m)x﹣m2,即x2+2(m﹣1)x+m2=0的两根,
∴y=x1+x2=﹣2m+2,且m≤![]() ; 因而y随m的增大而减小,故当m=
; 因而y随m的增大而减小,故当m=![]() 时,取得最小值1.
时,取得最小值1.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】计算下列各题.
(1)﹣1.3+(﹣1.7)﹣(﹣13)
(2)﹣30×( ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )
)
(3)(﹣2)2×3+2×(﹣32)
(4)﹣2×( ![]() ﹣
﹣ ![]() )+|﹣7|.
)+|﹣7|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】a为有理数.定义符号“※”:当a>﹣2时,※a=﹣a;当a<﹣2时,※a=a;当a=﹣2时,※a=0.根据这种定义.则※[﹣4+※(2﹣3)]的值为( )
A. 3 B. ﹣3 C. 5 D. ﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1或5 △ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为
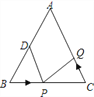
A. 2 B. 3 C. 2或3 D. 1或5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于变量x,y的关系式中:①3x-2y=5;②y=|x|;③2x-y2=10.其中y是x的函数的是( )
A. ①②③ B. ①② C. ①③ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句正确的个数是( )
①不相交的两条直线叫做平行线;②两点之间直线最短;③只有一个公共点的两条直线叫做相交直线;④两点确定一条直线.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】义务教育均衡发展是一种新的教育发展观,是解决我国目前教育问题的新举措.其最终目标,就是要合理配置教育资源,办好每一所学校,教好每一个学生,实现教育公平.我们县级政府为推进义务教育均衡发展工作的评估,今年预算办学经费约为3亿5千万,请你用科学记数法表示应是( )
A.3.5×108
B.3.5×109
C.35×108
D.0.35×109
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com