
【题目】探究:如图1,在△ABC中,AB=AC,CF为AB边上的高,点P为BC边上任意一点,PD⊥AB,PE⊥AC,垂足分别为点D,E.求证:PD+PE=CF.
嘉嘉的证明思路:连结AP,借助△ABP与△ACP的面积和等于△ABC的面积来证明结论.
淇淇的证明思路:过点P作PG⊥CF于G,可证得PD=GF,PE=CG,则PD+PE=CF.
迁移:请参考嘉嘉或淇淇的证明思路,完成下面的问题:
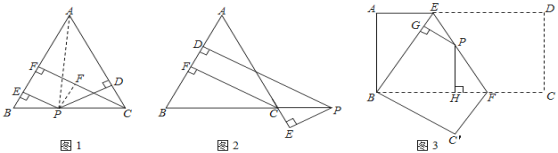
(1)如图2.当点P在BC延长线上时,其余条件不变,上面的结论还成立吗?若不成立,又存在怎样的关系?请说明理由;
(2)当点P在CB延长线上时,其余条件不变,请直接写出线段PD,PE和CF之间的数量关系.
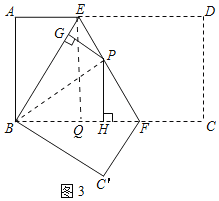
运用:如图3,将矩形ABCD沿EF折叠,使点D落在点B处,点C落在点C′处.若点P为折痕EF上任一点,PG⊥BE于G,PH⊥BC于H,若AD=18,CF=5,直接写出PG+PH的值.
【答案】(1)不成立,CF=PD-PE,理由见解析;(2)CF=PE-PD理由见解析;运用:PG+PH的值为12.
【解析】
(1)由三角形的面积和差关系可求解;
(2)由三角形的面积和差关系可求解;
(3)易证BE=BF,过点E作EQ⊥BF,垂足为Q,利用探究中的结论可得PG+PH=EQ,易证EQ=AB,BF=BE=DE=13,只需求出AB即可.
解:(1)不成立,CF=PD-PE
理由如下:
连接AP,如图,

∵PD⊥AB,PE⊥AC,CF⊥AB,
且S△ABC=S△ABP-S△ACP,
∴![]() ABCF=
ABCF=![]() ABPD-
ABPD-![]() ACPE.
ACPE.
∵AB=AC,
∴CF=PD-PE.
(2)CF=PE-PD
理由如下:
如图,
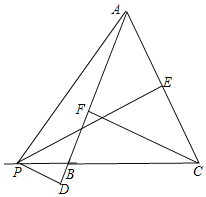
∵S△ABC=S△ACP-S△ABP,
∴![]() ABCF=
ABCF=![]() ACPE-
ACPE-![]() ABPD
ABPD
∵AB=AC
∴CF=PE-PD
运用:过点E作EQ⊥BC,垂足为Q,如图,
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,∠A=∠ABC=90°.
∵AD=18,CF=5,
∴BF=BC-CF=AD-CF=13.
由折叠可得:DE=BB,∠BEF=∠DEF.
∵AD∥BC
∴∠DEF=∠EFB
∴∠BEF=∠BFE
∴BE=BF=13=DE
∴AE=5
∵∠A=90°,
∴AB=![]() =12
=12
∵EQ⊥BC,∠A=∠ABC=90°.
∴∠EQC=90°=∠A=∠ABC
∴四边形EQBA是矩形.
∴EQ=AB=12.
由探究的结论可得:PG+PH=EQ.
∴PG+PH=12.
∴PG+PH的值为12.
故答案为:(1)不成立,CF=PD-PE,理由见解析;(2)CF=PE-PD理由见解析;运用:PG+PH的值为12.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点E是边AC上一点,线段BE垂直于∠BAC的平分线于点D,点M为边BC的中点,连接DM.
(1)求证: DM=![]() CE;
CE;
(2)若AD=6,BD=8,DM=2,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解油价上涨给出租车行业带来的成本压力,某市拟调整出租车运价,调整方案见下列表格及图象(其中![]() 为常数)
为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过 | 起步价7元 | 起步价 |
超过 | 每公里2元 | 每公里 |
超出 | 每公里 | |
设行驶路程为![]() ,调价前的运价
,调价前的运价![]() (元),调价后运价
(元),调价后运价![]() (元),如图,折线
(元),如图,折线![]() 表示
表示![]() 与
与![]() 之间的函数关系式,线段
之间的函数关系式,线段![]() 表示当
表示当![]() 时,
时,![]() 与
与![]() 的函数关系式,根据图表信息,完成下列各题:
的函数关系式,根据图表信息,完成下列各题:
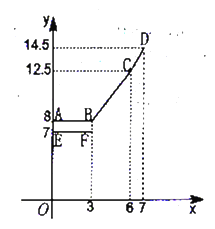
①填空:![]() ,
,![]() ,
,![]() ;
;
②当![]() 时,求
时,求![]() 与
与![]() 的关系,补充图中该函数的图像;
的关系,补充图中该函数的图像;
③函数![]() 与
与![]() 的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的面积等于25,直线a,b,c分别过A,B,C三点,且a∥b∥c,EF⊥直线c,垂足为点F交直线a于点E,若直线a,b之间的距离为3,则EF=( )
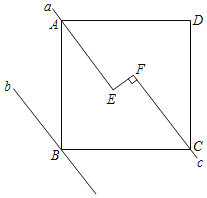
A. 1B. 2C. ![]() -3D. 5-
-3D. 5-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 为菱形,
为菱形,![]() ,
,![]() ,
,![]() 的两边分别与射线
的两边分别与射线![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() ,且
,且![]() .
.
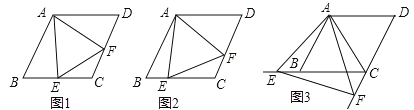
(1)如图1,当点![]() 是线段
是线段![]() 的中点时,请直接写出线段
的中点时,请直接写出线段![]() 与
与![]() 之间的数量关系;
之间的数量关系;
(2)如图2,当点![]() 是线段
是线段![]() 上的任意一点(点
上的任意一点(点![]() 不与点
不与点![]() 、
、![]() 重合)时,求证:
重合)时,求证:![]() ;
;
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() 时,求线段
时,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球训练中,为了训练球员快速抢断转身,教练设计了折返跑训练.教练在东西方向的足球场上画了一条直线插上不同的折返旗帜,如果约定向西为正,向东为负,练习一组的行驶记录如下(单位:米):+40,-30,+50,-25,+25,-30,+15,-28,+16,-20.
(1)球员最后到达的地方在出发点的哪个方向?距出发点多远?
(2)球员训练过程中,最远处离出发点多远?
(3)球员在一组练习过程中,跑了多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com