练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】梯形ABCD中AD∥BC ， E是AB的中点，过E作两底的平行线交DC于F ， 则下面结论错误的是（　　）
    A.EF平分线段AC
    B.梯形上下底间任意两点的连线段被EF平分
    C.梯形EBCF与梯形AEFD周长之差的绝对值等于梯形两底之差的绝对值
    D.梯形EBCF的面积比梯形AEFD的面积大

    【答案】D
    【解析】解答：根据题意可知EF是梯形ABCD的中位线，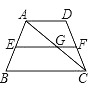
    则A正确，因为EF是梯形ABCD的中位线，所以FG是△ACD的中位线，则EF平分线段AC.
    B正确，因为EF是梯形ABCD的中位线，再根据平行线分线段成比例，则梯形上下底间任意两点的连线段被EF平分 ．
    C正确，因为梯形EBCF的周长为EF+EB+BC+CF ， 梯形AEFD周长为AE+AD+DF+EF ， 又因为EF是梯形ABCD的中位线，所以梯形EBCF与梯形AEFD周长之差的绝对值等于梯形两底之差的绝对值 ．
    D错误，因为根据题意不能判断AD和BC谁是上底谁是下底，所以不能判断梯形EBCF的面积比梯形AEFD的面积大 ．
    故选D.
    分析：根据题意可先判断出EF是梯形ABCD的中位线，然后再根据梯形中位线的性质分别进行判断 ．
    【考点精析】掌握梯形的中位线是解答本题的根本，需要知道梯形的中位线平行于梯形的两底并等于两底和的一半．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知点A（0，1），B（-2，0），以坐标原点O为位似中心，将线段AB放大2倍，放大后的线段A′B′与线段AB在同一侧，则两个端点A′，B′的坐标分别为.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AD⊥BC于D，若BD=AD，FD=CD．猜想：BF与AC的关系，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】三种不同类型的纸板的长宽如图所示，其中A类和C类是正方形，B类是长方形，现A类有1块，B类有4块，C类有5块. 如果用这些纸板拼成一个正方形，发现多出其中1块纸板，那么拼成的正方形的边长是（ ）

    A. m+n B. 2m+2n C. 2m+n D. m+2n

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，在△ABC中三个内角的度数满足∠ABC：∠C：∠A=5：6：7，BD是△ABC的角平分线，DE是△DBC的高.

    （1）求△ABC各内角的度数；

    （2）求图中的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,已知矩形ABCD,点E为BC的中点,将△ABE沿直线AE折叠,点B落在B′点处,连接B′C

    (1)求证：AE∥B′C；

    (2)若AB=4,BC=6,求线段B′C的长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A=∠ABD，若AC=5，BC=3，则BD的长为（　　）

    A. 1 B. C. D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校有一块长方形活动场地，长为米，宽比长少米，实施“阳光体育”行动以后，学校为了扩大学生的活动场地，让学生能更好地进行体育活动，将操场的长和宽都增加米.

    （1）求活动场地原来的面积是多少平方米.（用含的代数式表示）

    （2）若，求活动场地面积增加后比原来多多少平方米.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，如图所示，△AOB是边长为2的等边三角形，将△AOB绕着点B按顺时针方向旋转得到△DCB，使得点D落在x轴的正半轴上，连接OC、AD．
    （1）求证：OC=AD；
    （2）求OC的长．

    查看答案和解析>>

    同步练习册答案