
 保护视力要求人写字时眼睛和笔端的距离应超过30cm,图1是一位同学的坐姿,把他的眼睛B,肘关节C和笔端A的位置关系抽象成图2的△ABC,已知BC=30cm,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
保护视力要求人写字时眼睛和笔端的距离应超过30cm,图1是一位同学的坐姿,把他的眼睛B,肘关节C和笔端A的位置关系抽象成图2的△ABC,已知BC=30cm,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3) 分析 根据锐角三角函数关系得出BD,DC的长,进而结合勾股定理得出答案.
解答  解:他的这种坐姿不符合保护视力的要求,
解:他的这种坐姿不符合保护视力的要求,
理由:如图2所示:过点B作BD⊥AC于点D,
∵BC=30cm,∠ACB=53°,
∴sin53°=$\frac{BD}{BC}$=$\frac{BD}{30}$≈0.8,
解得:BD=24,
cos53°=$\frac{DC}{BC}$≈0.6,
解得:DC=18,
∴AD=22-18=4(cm),
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{{4}^{2}+2{4}^{2}}$=$\sqrt{592}$<$\sqrt{900}$,
∴他的这种坐姿不符合保护视力的要求.
点评 此题主要考查了解直角三角形的应用,根据题意得出BD,AD的长是解题关键.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届浙江省平阳县名校九年级下学期第一次模拟统练数学试卷(解析版) 题型:单选题
如图是六个相同的小正方体组成的几何体,其左视图是( )
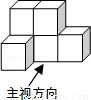
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com