
 ID•AI•sin60°=
ID•AI•sin60°= ×2×2×
×2×2×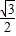 =
=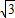 ,进而可得出结论;
,进而可得出结论; =
= ,再根据圆周角定理即可得出IA=IB',DA=DA',进而可得出结论.
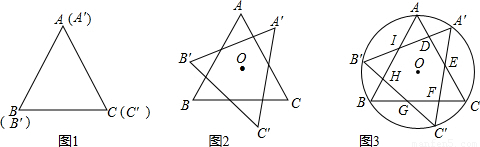
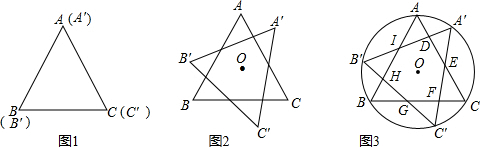
,再根据圆周角定理即可得出IA=IB',DA=DA',进而可得出结论.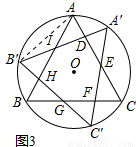 解:(1)∵当B′与A重合时正△A'B'C'与正△ABC出现旋转过程中的第一次完全重合,此时点A′与C重合,旋转角度α=180°-60°=120°,
解:(1)∵当B′与A重合时正△A'B'C'与正△ABC出现旋转过程中的第一次完全重合,此时点A′与C重合,旋转角度α=180°-60°=120°, ID•AI•sin60°=
ID•AI•sin60°= ×2×2×
×2×2× =
= ,
,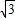 (7分)
(7分)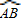 =
=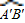 ,
,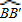 =
= ,(9分)
,(9分)

科目:初中数学 来源: 题型:
 20、如图,在边长均为l的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.
20、如图,在边长均为l的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:
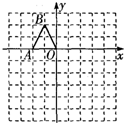
 21、如图,在边长均为1的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.
21、如图,在边长均为1的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:
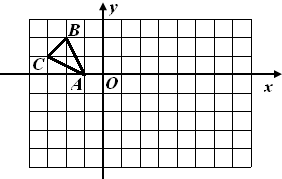 23、如图,在边长均为l的小正方形网格纸中,△ABC的顶点A、B、C均在格点上,O为直角坐标系的原点,点A(-1,0)在x轴上.
23、如图,在边长均为l的小正方形网格纸中,△ABC的顶点A、B、C均在格点上,O为直角坐标系的原点,点A(-1,0)在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在边长均为1的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,
如图,在边长均为1的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com