
分析 (1)首先根据?(加乘)运算的运算法则进行运算的算式,归纳出?(加乘)运算的运算法则即可;然后根据:0?(+8)=8;(-6)?0=6,可得:0和任何数进行?(加乘)运算,或任何数和0进行?(加乘)运算,等于这个数的绝对值.
(2)根据(1)中总结出的?(加乘)运算的运算法则,以及有理数的混合运算的运算方法,求出(-2)?[0?(-1)]的值是多少即可.
(3)加法有交换律和结合律,这两种运算律在有理数的?(加乘)运算中还适用,并举例验证加法交换律适用即可.
解答 解:(1)归纳?(加乘)运算的运算法则:
两数进行?(加乘)运算时,同号得正,异号得负,并把绝对值相加.
特别地,0和任何数进行?(加乘)运算,或任何数和0进行?(加乘)运算,等于这个数的绝对值.
(2)(-2)?[0?(-1)]
=(-2)?1
=-3
(3)加法交换律和加法结合律在有理数的?(加乘)运算中还适用.
由?(加乘)运算的运算法则可知:
(+5)?(+2)=+7,
(+2)?(+5)=+7,
所以(+5)?(+2)=(+2)?(+5),
即加法交换律在有理数的?(加乘)运算中还适用.
故答案为:同号得正,异号得负,并把绝对值相加;等于这个数的绝对值;-3.
点评 此题主要考查了定义新运算,以及有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算,注意加法运算定律的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
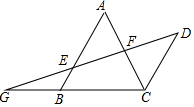 如图.△ABC中,AB=BC=4,CD∥AB,过D点的直线交AC、AB于点F、E,交CB的延长线于点G,DF=EF.
如图.△ABC中,AB=BC=4,CD∥AB,过D点的直线交AC、AB于点F、E,交CB的延长线于点G,DF=EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com