

分析 (1)作一条射线,截取BC=a,作出线段BC的垂直平分线,垂足为D,截取AD=b,连接AB,AC,三角形ABC为所求的三角形;
(2)由三线合一求出BD的长,在直角三角形ABD中,利用勾股定理求出AB的长,设腰AB上的高为h,利用面积法求出h即可.
解答 解:(1)如图所示:
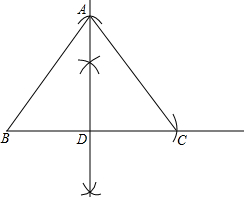
则△ABC为所求的三角形;
(2)∵△ABC为等腰三角形,AD⊥BC,
∴BD=CD=$\frac{1}{2}$BC=$\frac{1}{2}$a=3,
在Rt△ABD中,BD=3,AD=b=4,
根据勾股定理得:AB=5,
设腰AB边上的高为h,
由题意得:$\frac{1}{2}$AB•h=$\frac{1}{2}$BC•AD,
解得:h=$\frac{BC•AD}{AB}$=$\frac{6×4}{5}$=$\frac{24}{5}$.
点评 此题考查了作图-复杂作图,以及等腰三角形的性质,尺规作图时注意保留作图痕迹,不写画法,熟练掌握等腰三角形的性质是解本题第二问的关键.


科目:初中数学 来源: 题型:选择题
| A. | $4-2\sqrt{3}$ | B. | $2-\sqrt{3}$ | C. | $\sqrt{3}-1$ | D. | $\frac{1}{2}(\sqrt{3}-1)$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,Rt△AOB的两条直角边OA、OB分别在x轴的负半轴、y轴的负半轴上,且OA=2,OB=1.将Rt△AOB绕点O按顺时针方向旋转90°,再把所得的像沿x轴正方向平移1个单位,得△CDO.
如图,在直角坐标系中,Rt△AOB的两条直角边OA、OB分别在x轴的负半轴、y轴的负半轴上,且OA=2,OB=1.将Rt△AOB绕点O按顺时针方向旋转90°,再把所得的像沿x轴正方向平移1个单位,得△CDO.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,小明将一块矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=3:5,则sin∠EFA的值是( )
如图,小明将一块矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=3:5,则sin∠EFA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A(-1,0),C(1,4),点B在x轴上,且AB=3.
如图,A(-1,0),C(1,4),点B在x轴上,且AB=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,圆柱形容器高为16cm,底面周长为24cm,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点A处,则蚂蚁A处到达B处的最短距离为多少?
如图,圆柱形容器高为16cm,底面周长为24cm,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点A处,则蚂蚁A处到达B处的最短距离为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
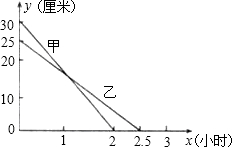 在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
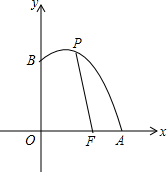 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,P是此图象上的一动点.设P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,P是此图象上的一动点.设P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com