
 如图所示,在正方形ABCD的对角线BD上取一点E,使得∠BAE=15°,连接AE、CE,延长CE到F,连接BF,使得BC=BF.若AB=1,有下列结论:①AE=EC;②F到BC的距离为$\frac{\sqrt{2}}{2}$;③BE+EC=EF;④S△EBF=$\frac{\sqrt{3}}{12}$.其中正确结论的序号是①③④.
如图所示,在正方形ABCD的对角线BD上取一点E,使得∠BAE=15°,连接AE、CE,延长CE到F,连接BF,使得BC=BF.若AB=1,有下列结论:①AE=EC;②F到BC的距离为$\frac{\sqrt{2}}{2}$;③BE+EC=EF;④S△EBF=$\frac{\sqrt{3}}{12}$.其中正确结论的序号是①③④. 分析 根据正方形的性质推出AB=BC,∠ABD=∠CBD=45,证△ABE≌△CBE,即可判断①;过F作FH⊥BC于H,根据直角三角形的性质即可求出FH;过A作AM⊥BD交于M,根据勾股定理求出BD,根据三角形的面积公式即可求出高AM,根据三角形的面积公式求出即可.
解答 解:∵正方形ABCD,
∴AD=DC,∠ADB=∠CDB=45°,
在△ABE和△CBE中,
$\left\{\begin{array}{l}{DA=DC}\\{∠ADB=∠CDB}\\{DE=DE}\end{array}\right.$,
∴△ABE≌△CBE,
∴AE=CE,∴①正确;
∵过F作FH⊥BC交CB的延长线于H,
∵BF=BC=1,
∴∠BFC=∠FCB=15°,
∴∠FBH=30°,
∴FH=$\frac{1}{2}$BF=$\frac{1}{2}$,∴②错误;
在EF上取一点N,使BN=BE,
又∵∠BEN=∠EBC+∠ECB=45°+15°=60°,
∴△NBE为等边三角形,
∴∠ENB=60°,
又∵∠NFB=15°,
∴∠NBF=45°,
又∵∠EBC=45°,
∴∠NBF=∠EBC,
在△FBN和△CBE中,
$\left\{\begin{array}{l}{∠NBF=∠EBC}\\{BF=BC}\\{∠NFB=∠ECB}\end{array}\right.$,
又∵BF=BC,∠NFB=∠ECB=15°,
∴△FBN≌△CBE,
∴NF=EC,
故BE+EC=EN+NF=EF,∴③正确;
作AM⊥BC,
∵AB=1,
∴BM=$\frac{1}{2}$BD=$\frac{\sqrt{2}}{2}$,
∵∠AEM=60°,
∴EM=$\frac{AM}{tan∠AEM}$=$\frac{\sqrt{6}}{6}$,
∴S△AEM=$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{6}}{6}$=$\frac{\sqrt{3}}{12}$,
∴S△ABE=$\frac{1}{4}$-$\frac{\sqrt{3}}{12}$,
∴S△CBE=S△ABE=$\frac{1}{4}$-$\frac{\sqrt{3}}{12}$,
∵S△CBF=$\frac{1}{2}×$1×$\frac{1}{2}$=$\frac{1}{4}$,
∴S△EBF=$\frac{\sqrt{3}}{12}$,④正确,
故答案为:①③④.
点评 本题主要考查对正方形的性质,全等三角形的性质和判定,三角形的面积,勾股定理,含30度角的直角三角形的性质等知识点的理解和掌握,综合运用这些性质进行证明是解此题的关键.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:解答题
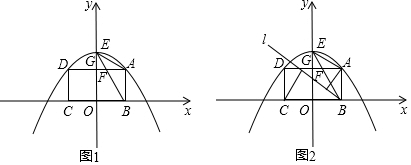
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
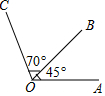 已知:如图,∠AOB=45°,∠BOC=70°,求∠AOC的度数.
已知:如图,∠AOB=45°,∠BOC=70°,求∠AOC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
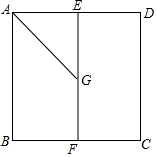 在边长为1的正方形ABCD中,点E,F分别是边AD,BC的中点,动点G在线段EF上运动,将线段AG绕点G顺时针旋转60°得到线段HG.
在边长为1的正方形ABCD中,点E,F分别是边AD,BC的中点,动点G在线段EF上运动,将线段AG绕点G顺时针旋转60°得到线段HG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
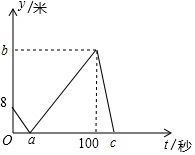 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步600米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则b=192.
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步600米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则b=192.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<b | B. | a>b | C. | a≤b | D. | a≥b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com