
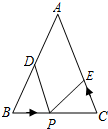
 如图,已知△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点E在线段CA上由C点向A点运动.当点E的运动速度为多少厘米/秒时,能够在某一时刻使△BPD与△CEP全等.
如图,已知△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点E在线段CA上由C点向A点运动.当点E的运动速度为多少厘米/秒时,能够在某一时刻使△BPD与△CEP全等. 分析 设点E运动的时间为t,点E运动的速度为xcm/s,则BP=4t,PC=16-4t,CE=tx,由于∠B=∠C,若CP=BD,CE=BP时,△BPD≌△CEP,即16-4t=12,tx=4t;若CP=BP,CE=BD时,△BPD≌△CPE,即16-4t=4t,tx=12,然后分别解方程求出x即可.
解答 解:设点E运动的时间为t,点E运动的速度为xcm/s,则BP=4t,PC=16-4t,CE=tx,
∵点D为AB的中点,
∴BD=$\frac{1}{2}$AB=12,
∵∠B=∠C,
∴当CP=BD,CE=BP时,可根据“SAS”判断△BPD≌△CEP,即16-4t=12,tx=4t,解得t=1,x=4;
当CP=BP,CE=BD时,可根据“SAS”判断△BPD≌△CPE,即16-4t=4t,tx=12,解得t=2,x=6,
综上所述,当点E的运动速度为4厘米/秒或6厘米/秒时,能够在某一时刻使△BPD与△CEP全等.
点评 本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -0.3>-$\frac{1}{3}$ | B. | (-2)2<(-2)3 | C. | (-2)2>-32 | D. | -$\frac{9}{10}$<-$\frac{8}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在六边形ABCDEF中,CM,DM分别平分∠BCD和∠CDE,若∠A+∠B+∠E+∠F=510°,则∠M的度数为( )
如图,在六边形ABCDEF中,CM,DM分别平分∠BCD和∠CDE,若∠A+∠B+∠E+∠F=510°,则∠M的度数为( )| A. | 85° | B. | 80° | C. | 75° | D. | 70° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=DE,AC=DF,∠A=∠D | B. | ∠A=∠D,∠B=∠E,AC=DF | ||
| C. | AB=DE,BC=EF,∠C=∠F | D. | AB=DE,AC=DF,BC=EF |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com