
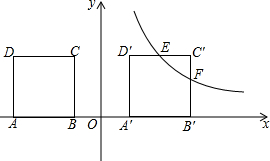
 ��ͼ����ƽ��ֱ������ϵ�У�������ABCD����D��-3��2����B��1��0����CD��x�ᣬ��������ABCD����ƽ��m����λ����������A��B��C��D�䣮�� m=4ʱ������������y=$\frac{k}{x}$��x��0����ͼ����߶�C��D����е�E�����߶�B��C�佻�ڵ�F��
��ͼ����ƽ��ֱ������ϵ�У�������ABCD����D��-3��2����B��1��0����CD��x�ᣬ��������ABCD����ƽ��m����λ����������A��B��C��D�䣮�� m=4ʱ������������y=$\frac{k}{x}$��x��0����ͼ����߶�C��D����е�E�����߶�B��C�佻�ڵ�F������ ��1�������E�����꣬���뷴���������Ľ���ʽ���ɣ�
��2�����ݷ���������y=$\frac{4}{x}$��x��0����ͼ�����C��ʱm��С��������D��ʱm��ɵó����ۣ�
��3�������ô���ϵ�������ֱ��EF�Ľ���ʽ�����������C������ֱ��EFƽ�е�ֱ�ߣ�����ͬ�ȸߵ��������������������ֱ���뷴���������Ľ��㼴�ɵó����ۣ�
��� �⣺��1���ߵ�EǡΪ�߶�C��D����е㣬
��C�䣨3��2����D�䣨1��2����
���E��2��2����
��E��2��2�����뷴��������y=$\frac{k}{x}$��x��0������k=4��
�෴������������ʽΪy=$\frac{4}{x}$��
��2���߷���������y=$\frac{4}{x}$��x��0����ͼ��ֱ����߶�C��D�䡢B��C��ͬʱ�н��㣬
�෴��������y=$\frac{4}{x}$��x��0����ͼ�����C�䣬
�ߵ�C���������Ϊ2��
��x=2��
��C�䣨2��2����
��C��-1��2����
��m=3��
����D���ƶ�����2��2��ʱ��m���
��D��-3��2����
��m=2+3=5��
��3��m��5��
��D��-3��2����
�൱m=4ʱ��-3+4=1��
��D��1��2����
�ʴ�Ϊ��3��m��5����1��2����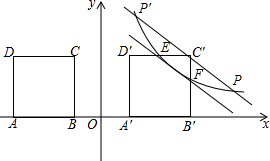
��3�����ڣ�
���ɣ���ͼ��ʾ����ֱ��EF�Ľ���ʽΪy=kx+b��k��0����
�ߵ�E��2��2������F��3��$\frac{4}{3}$����
��$\left\{\begin{array}{l}2=2k+b\\ \frac{4}{3}=3k+b\end{array}\right.$�����$\left\{\begin{array}{l}k=-\frac{2}{3}\\ b=\frac{10}{3}\end{array}\right.$��
��ֱ��EF����ʽy=-$\frac{2}{3}$x+$\frac{10}{3}$��
��C�����EFƽ�е�ֱ��y=-$\frac{2}{3}$x+4��
��$\left\{\begin{array}{l}y=-\frac{2}{3}x+4\\ y=\frac{4}{x}\end{array}\right.$�����$\left\{\begin{array}{l}{x}_{1}=3+\sqrt{3}\\{x}_{2}=3-\sqrt{3}\end{array}\right.$��
�ߵ�x=3+$\sqrt{3}$ʱ��y=$\frac{4}{3+\sqrt{3}}$=2-$\frac{2\sqrt{3}}{3}$����x=3-$\sqrt{3}$ʱ��y=$\frac{4}{3-\sqrt{3}}$=2+$\frac{2\sqrt{3}}{3}$��
��P��3+$\sqrt{3}$��2-$\frac{2\sqrt{3}}{3}$����P�䣨3-$\sqrt{3}$��2+$\frac{2\sqrt{3}}{3}$����
���� ���⿼����Ƿ����������ۺ��⣬�漰������������ͼ���ϵ�������ص㡢�����ε����ʼ�����ϵ������һ�κ����Ľ���ʽ��֪ʶ���Ѷ����У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
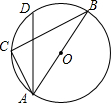 ��ͼ����ABC�ڽ��ڡ�O��ABΪO��ֱ������CAB=60�㣬��ADƽ�֡�CAB����AD=3����AC=$\sqrt{3}$��
��ͼ����ABC�ڽ��ڡ�O��ABΪO��ֱ������CAB=60�㣬��ADƽ�֡�CAB����AD=3����AC=$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
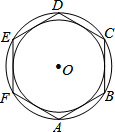 ��ͼ����������ABCDEF�ı߳�Ϊ2������������ε����Բ������Բ���γɵ�Բ�����Ϊ�У�
��ͼ����������ABCDEF�ı߳�Ϊ2������������ε����Բ������Բ���γɵ�Բ�����Ϊ�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪������y=ax2-4ax+3��ֱ��y=bx-4b+3�ཻ��һ����A��
��֪������y=ax2-4ax+3��ֱ��y=bx-4b+3�ཻ��һ����A���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ��ͼ����������y=ax2+2ax+a2+2��һ���֣�����x���һ������A�������ǣ�-3��0����������x�����һ�����������Ϊ��1��0����
��ͼ��ʾ��ͼ����������y=ax2+2ax+a2+2��һ���֣�����x���һ������A�������ǣ�-3��0����������x�����һ�����������Ϊ��1��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
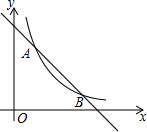 ��ͼ��һ�κ���y=kx+b��k��bΪ��������k��0����ͼ���뷴��������y=$\frac{3}{x}$��ͼ����A��1��a����B��3��1�����㣮
��ͼ��һ�κ���y=kx+b��k��bΪ��������k��0����ͼ���뷴��������y=$\frac{3}{x}$��ͼ����A��1��a����B��3��1�����㣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com