
 ,
, ,x2=-1-
,x2=-1- ;
; ;
; =
= ,
, ,x2=
,x2= .
.

科目:初中数学 来源: 题型:阅读理解
| pq+1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| pq+1 |
| q |
| 1 |
| n2 |
| 5 |
| n |
| 1 |
| m |
| 1 |
| n |
查看答案和解析>>
科目:初中数学 来源: 题型:
 “数形结合”是一种极其重要的思想方法.例如,我们可以利用数轴解分式不等式
“数形结合”是一种极其重要的思想方法.例如,我们可以利用数轴解分式不等式| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
查看答案和解析>>
科目:初中数学 来源:数学课外练习八年级下学期使用 题型:044
| |||||||||||||||||||||||||||||||||||||||||
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省九年级10月月考数学试卷(解析版) 题型:解答题
阅读材料:已知方程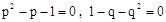 且
且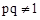 ,求
,求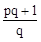 的值.
的值.
解:由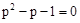 ,及
,及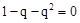 可知
可知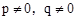 ,又∵
,又∵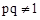 ,∴
,∴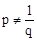 .
.
∵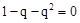 可变形为
可变形为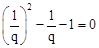 ,根据
,根据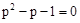 和
和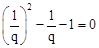 的特征.
的特征.
∴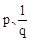 是方程
是方程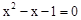 的两个不相等的实数根,则
的两个不相等的实数根,则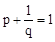 ,即
,即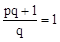 .
.
根据阅读材料所提供的方法,完成下面的解答.
已知: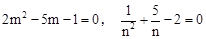 ,且
,且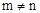 ,求下列各式的值(1)
,求下列各式的值(1)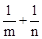 ;(2)
;(2)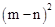 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com