
【题目】(8分)如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,﹣2),反比例函数![]() 的图象经过点C,一次函数
的图象经过点C,一次函数![]() 的图象经过A、C两点.
的图象经过A、C两点.

(1)求反比例函数与一次函数的解析式;
(2)求反比例函数与一次函数的另一个交点M的坐标;
(3)若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
【答案】(1)![]() ,
,![]() ;(2)M(﹣2,3);(3)P(18,
;(2)M(﹣2,3);(3)P(18,![]() )或(﹣18,
)或(﹣18,![]() ).
).
【解析】
试题(1)先由A点和B点坐标得到正方形的边长,于是可得到C的坐标,然后利用待定系数法求反比例函数与一次函数的解析式即可;
(2)通过解关于反比例函数解析式与一次函数的解析式所组成的方程组可得到M点的坐标;
(3)设P(t,![]() ),由三角形面积公式和正方形面积公式得到
),由三角形面积公式和正方形面积公式得到![]() ×1×|t|=3×3,然后解绝对值方程求出t即可得到P点坐标.
×1×|t|=3×3,然后解绝对值方程求出t即可得到P点坐标.
试题解析:(1)∵点A的坐标为(0,1),点B的坐标为(0,﹣2),∴AB=1+2=3,∵四边形ABCD为正方形,∴Bc=3,∴C(3,﹣2),把C(3,﹣2)代入![]() ,得k=3×(﹣2)=﹣6,∴反比例函数解析式为
,得k=3×(﹣2)=﹣6,∴反比例函数解析式为![]() ,把C(3,﹣2),A(0,1)代入
,把C(3,﹣2),A(0,1)代入![]() ,得
,得![]() ,解得:
,解得:![]() ,∴一次函数解析式为
,∴一次函数解析式为![]() ;
;
(2)解方程组 ,得:
,得:![]() 或
或![]() ,∴M点的坐标为(﹣2,3);
,∴M点的坐标为(﹣2,3);
(3)设P(t,![]() ),∵△OAP的面积恰好等于正方形ABCD的面积,∴
),∵△OAP的面积恰好等于正方形ABCD的面积,∴![]() ×1×|t|=3×3,解得t=18或t=﹣18,∴P点坐标为(18,
×1×|t|=3×3,解得t=18或t=﹣18,∴P点坐标为(18,![]() )或(﹣18,
)或(﹣18,![]() ).
).



科目:初中数学 来源: 题型:
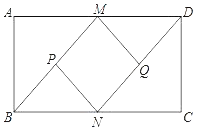
【题目】已知:如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)求证:BM∥DN;
(2)求证:四边形MPNQ是菱形;
(3)矩形ABCD的边长AB与AD满足什么数量关系时四边形MPNQ为正方形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球(不放回),再从余下的2个球中任意摸出1个球.
(1)用树状图或列表等方法列出所有可能出现的结果;
(2)求两次摸到的球的颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数y=![]() 的图象于点B,AB=
的图象于点B,AB=![]() .
.
(1)求反比例函数的解析式;
(2)若P(x1,y1)、Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,指出点P、Q各位于哪个象限?并简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,
,![]() 试说明直线AD与BC垂直
试说明直线AD与BC垂直![]() 请在下面的解答过程的空格内填空或在括号内填写理由
请在下面的解答过程的空格内填空或在括号内填写理由![]() .
.

理由:![]() ,
,![]() 已知
已知![]()
![]() ______
______![]() ______,
______,![]() ______
______![]()
![]() ______
______![]() ______
______![]()
又![]() ,
,![]() 已知
已知![]()
![]() ______
______![]() 等量代换
等量代换![]()
![]() ______
______![]() ______,
______,![]() ______
______![]()
![]() ______
______![]()
![]() ,
,![]() 已知
已知![]()
![]() ,
,![]() ,
,
![]() ______
______![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
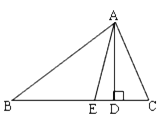
【题目】如图所示,△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=40°,∠C=70°,求∠DAE的度数,并说明理由;
(2)若∠B=α,∠C=β(α<β),请你根据(1)问的结果大胆猜想∠DAE与α,β间的等量关系 .(不需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
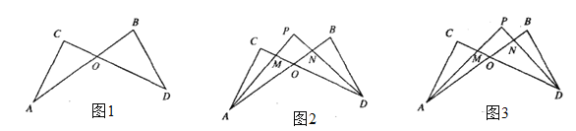
【题目】如图1,线段AB、CD相交于点O,连结AC、BD,我们把形如图1的图形称之为“8字形”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥聪明才智,解决以下问题:
(1)在图1中,请写出∠A、∠B、∠C、∠D之间的数量关系,并说明理由;
(2)仔细观察,在图2中“8字形”的个数有 个;
(3)在图2中,若∠B=70°,∠C=84°,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N利用(1)的结论,试求∠P的度数;
(4)在图3中,如果∠B和∠C为任意角,并且AP和DP分别是∠CAB和∠BDC的四等分线,即∠PAO=![]() ∠CAO, ∠BDP=
∠CAO, ∠BDP=![]() ∠BDO,那么∠P与∠C、∠B之间存在的数量关系是 (直接写出结论即可).
∠BDO,那么∠P与∠C、∠B之间存在的数量关系是 (直接写出结论即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:

如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(______________ _________),
∴∠2 =∠CGD(等量代换).
∴CE∥BF(___________________ ________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD(________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的方格地面上,标有编号A,B,C的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同.
(1)一只自由飞行的鸟,将随意地落在图中的方格地面上,问小鸟落在草坪上的概率是多少?
(2)现从3个小方格空地中任意选取2个种植草坪,则刚好选取A和B的2个小方格空地种植草坪的概率是多少(用树形图或列表法求解)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com