【题目】如图所示，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（ ）
A.带①去B.带②去C.带③去D.带①和②去
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】已知，△ABC中，∠ACB＝90°，AC＝BC，点E是BC上一点，连接AE
（1）如图1，当AE平分∠BAC时，EH⊥AB于H，△EHB的周长为10m，求AB的长；
（2）如图2，延长BC至D，使DC＝BC，将线段AE绕点A顺时针旋转90°得线段AF，连接DF，过点B作BG⊥BC，交FC的延长线于点G，求证：BG＝BE．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有一座抛物线形拱桥，正常水位桥下面宽度为20米，拱顶距离水平面4米，如图建立直角坐标系，若正常水位时，桥下水深6米，为保证过往船只顺利航行，桥下水面宽度不得小于18米，则当水深超过多少米时，就会影响过往船只的顺利航行（ ）
A. 2.76米 B. 6.76米 C. 6米 D. 7米
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知直线l:y=kx+1与抛物线y=x2-4x
（1）求证：直线l与该抛物线总有两个交点；
（2）设直线l与该抛物线两交点为A，B，O为原点，当k=-2时，求△OAB的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
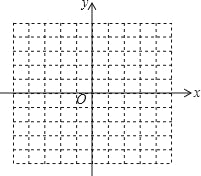
【题目】已知二次函数y=﹣x2+4x．
（1）写出二次函数y=﹣x2+4x图象的对称轴；
（2）在给定的平面直角坐标系中，画出这个函数的图象（列表、描点、连线）；
（3）根据图象，写出当y＜0时，x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC与△ADE中，∠BAC＝∠DAE＝90°，AD＝AE，AB＝AC，且B、D、E三点在一条直线上．
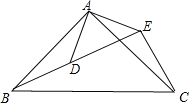
（1）求证：BD＝CE．
（2）求∠BEC的度数．
（3）写出BE与AE、CE的数量关系是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在直角坐标系中，△ABC三个顶点的坐标分别是A（1，1），B (4，2)，C(3，4)．
（1）请画出△ABC关于y轴对称的△
；
（2）△的面积为 ；
（3）在
轴上求作一点P，使△PAB周长最小，请画出△PAB，并直接写出点P的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，点E，F分别在四边形ABCD的边BC，CD上，∠EAF=
∠BAD，连接EF，试猜想EF，BE，DF之间的数量关系．
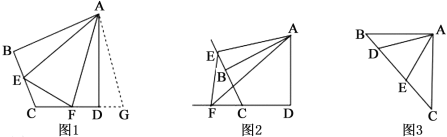
（1）思路梳理
将△ABE绕点A逆时针旋转至△ADG，使AB与AD重合，由∠B+∠ADC=180°，得∠FDG=180°，即点F，D，G三点共线，易证△AFG≌△AFE，故EF，BE，DF之间的数量关系为__；
（2）类比引申
如图2，在图1的条件下，若点E，F由原来的位置分别变到四边形ABCD的边CB，DC延长线上，∠EAF=∠BAD，连接EF，试猜想EF，BE，DF之间的数量关系，并给出证明．
（3）联想拓展
如图3，在△ABC中，∠BAC=90°，AB=AC，点D，E均在边BC上，且∠DAE=45°，若BD=1，EC=2，直接写出DE的长为________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
