
 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.分析 (1)连结EF交AC于O,如图,利用折叠的性质得EA=EC,FA=FC,再证明△AEF为等腰三角形得到AE=AF,则AE=EC=AF=CF,然后根据菱形的判定方法可判断四边形AFCE是菱形;
(2)先利用面积公式得到AB•BF=48,再利用勾股定理得到AB2+BF2=AF2=100,则利用完全平方公式可得到AB+BF=14,从而得计算出△ABF的周长;
(3)过点E作EP⊥AD交AC于P,此时P点为所作,利用∠EAO=∠POE,∠AOE=∠AEP可判断△AOE∽△AEP,则利用相似比得到AE2=AO•AP,由于OA=$\frac{1}{2}$AC,所以2AE2=AC•AP.
解答 (1)证明:连结EF交AC于O,如图,
∵将矩形ABCD(AD>AB)折叠,使点A与点C重合,
∴EF垂直平分AC,
∴EA=EC,FA=FC,
∴∠2=∠3,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠1=∠2,
∴∠1=∠3,
而AO⊥EF,
∴△AEF为等腰三角形,
∴AE=AF,
∴AE=EC=AF=CF,
∴四边形AFCE是菱形;
(2)解:在Rt△ABF中,∵$\frac{1}{2}$AB•BF=24,
∴AB•BF=48,
∵AF=AE=10,
∴AB2+BF2=AF2=100,
∴(AB+BF)2-2AB•BF=100,即(AB+BF)2-2•48=100,即
∴AB+BF=14,
∴△ABF的周长=AB+BF+AF=14+10=24(cm);
(3)解:存在.
过点E作EP⊥AD交AC于P,此时P点为所作,如图,则∠AEP=90°,
∵∠EAO=∠POE,∠AOE=∠AEP,
∴△AOE∽△AEP,
∴AO:AE=AE:AP,
∴AE2=AO•AP,
∵OA=$\frac{1}{2}$AC,
∴2AE2=AC•AP.
点评 本题考查了相似形综合题:熟练掌握折叠的性质、矩形的性质和菱形的判定方法;会利用勾股定理和相似比计算线段的长和表示线段之间的关系.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=$\frac{1}{n}$AD (n为大于2的整数),连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连接BF和EG.
如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=$\frac{1}{n}$AD (n为大于2的整数),连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连接BF和EG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
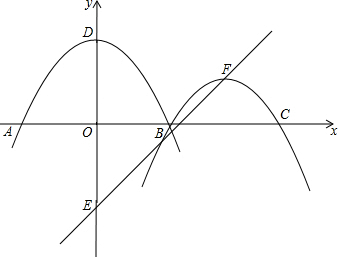 如图:二次函数y=ax2+c(a<0,c>0)的图象C1交
如图:二次函数y=ax2+c(a<0,c>0)的图象C1交查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=x+3与双曲线y=$\frac{m-3}{x}$( m为常数)交于点A(a,2)、B两点.
如图,直线y=x+3与双曲线y=$\frac{m-3}{x}$( m为常数)交于点A(a,2)、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
型号 金额 | Ⅰ型设备 | Ⅱ型设备 | |||
| 投资金额x(万元) | x | 5 | x | 2 | 4 |
| 补贴金额y(万元) | y1=kx(k≠0) | 2 | y2=ax2+bx(a≠0) | 2.8 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com