
分析 (1)设A品牌计算器的单价为a元,B品牌计算器的单价为b元,根据“购买2个A品牌和1个B品牌的计算器共需122元;购买1个A品牌和2个B品牌的计算器共需124元”即可得出关于a、b的二元一次方程组,解方程组即可得出结论;
(2)根据“购买A品牌计算器按原价的九折销售,购买B品牌计算器超出10个以上超出的部分按原价的八折销售”,即可得出y1、y2关于x的函数关系式;
(3)分别计算y1<y2、y1=y2、y1>y2得出x的取值范围,由此即可得出结论.
解答 解:(1)设A品牌计算器的单价为a元,B品牌计算器的单价为b元,
则由题意可知:$\left\{\begin{array}{l}{2a+b=122}\\{a+2b=124}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=40}\\{b=42}\end{array}\right.$,
答:A品牌计算器的单价为40元,B品牌计算器的单价为42元.
(2)由题意可知:y1=0.9×40x,即y1=36x,
当0<x≤10时,y2=42x;
当x>10时,y2=42×10+42(x-10)×0.8,即y2=33.6x+84.
∴y2=$\left\{\begin{array}{l}{42x(0≤x≤10)}\\{33.6x+84(x>10)}\end{array}\right.$.
(3)当购买数量超过10个时,y2=33.6x+84.
①当y1<y2时,36x<33.6x+84,
解得:x<35,
∴当购买数量超过10个而不足35个时,购买A品牌的计算器更合算;
②当y1=y2时,36x=33.6x+84,
解得:x=35,
∴当购买数量为35个时,购买两种品牌的计算器花费相同;
③当y1>y2时,36x>33.6x+84,
解得:x>35.
∴当购买数量超过35个时,购买B品牌的计算器更合算.
点评 本题考查了一次函数的应用,解题的关键是:(1)列出关于a、b的二元一次方程组;(2)根据数量关系找出函数关系式;(3)令y1<y2、y1=y2、y1>y2求出x的取值范围.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列出方程(或函数关系式)是关键.


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
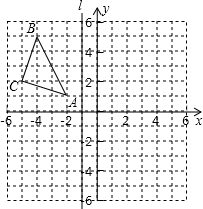 如图,△ABC在平面直角坐标系中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2),直线l经过点(-1,0)且和y轴平行.
如图,△ABC在平面直角坐标系中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2),直线l经过点(-1,0)且和y轴平行.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交$\widehat{BC}$于D.
如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交$\widehat{BC}$于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com