
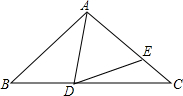
 如图,在等腰三角形ABC中,AB=AC,等边三角形ADE的顶点D,E分别落在AC,AC上,若AD=BD,求∠EDC的度数.
如图,在等腰三角形ABC中,AB=AC,等边三角形ADE的顶点D,E分别落在AC,AC上,若AD=BD,求∠EDC的度数. 分析 根据AB=AC,AD=BD,于是得到∠B=∠C=∠BAD,由于△ADE是等边三角形,得到∠AED=∠AED=∠DAE=60°,设∠B=∠C=∠BAD=y,根据三角形的内角和列方程求得y=40°,然后根据外角的性质即可得到结论.
解答 解:∵AB=AC,AD=BD,
∴∠B=∠C=∠BAD,
∵△ADE是等边三角形,
∴∠AED=∠AED=∠DAE=60°,
设∠B=∠C=∠BAD=y,
∴∠B+∠C+∠BAC=3y+60°=180°,
∴y=40°,
∴∠C=40°,
∵∠AED=∠EDC+∠C=60°,
∴∠EDC=20°.
点评 本题主要考查了等边三角形的性质,等腰三角形的判定和性质,等边对等角,等角对等边,正确确定相等关系列出方程是解题的关键.


科目:初中数学 来源: 题型:解答题
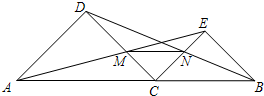 如图,已知C是线段AB上的任意一点(除端点外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连接AE交CD于点M,连接BD交CE于点N.
如图,已知C是线段AB上的任意一点(除端点外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连接AE交CD于点M,连接BD交CE于点N.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
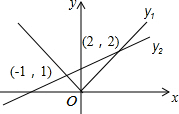 函数y1=|x|,y2=$\frac{1}{3}$x+$\frac{4}{3}$.当y1<y2时,x的范围是( )
函数y1=|x|,y2=$\frac{1}{3}$x+$\frac{4}{3}$.当y1<y2时,x的范围是( )| A. | x<-1 | B. | -1<x<2 | C. | x<-1或x>2 | D. | x>2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
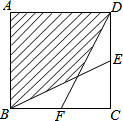 如图,正方形ABCD的边长为1cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是$\frac{2}{3}$ cm2.
如图,正方形ABCD的边长为1cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是$\frac{2}{3}$ cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 年龄 | 15岁 | 16岁 | 17岁 | 18岁 |
| 人 数 | 7 | 20 | 16 | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x+3y=5xy | B. | y3÷y3=1 | C. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D. | -$\sqrt{(-4)^{2}}$=-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 某校有教职工320名 | B. | 某次地震中,伤亡约10万人 | ||
| C. | 小明测得教室的长为6.5米 | D. | 一潜水艇处于海平面下约17米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com