
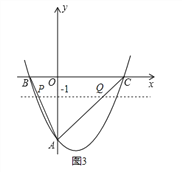
����Ŀ����ͼ��������A��0����4����������y=![]() x2+bx+c��x���ཻ��B����2��0����C������OΪ����ԭ����
x2+bx+c��x���ཻ��B����2��0����C������OΪ����ԭ����
��1���������ߵĽ���ʽ�����䷽����M��������
��2��������������һ��P��ʹ��PCB=��ABC����P��������
��3����������y=![]() x2+bx+c����ƽ��
x2+bx+c����ƽ��![]() ����λ������������ƽ��m��m��0������λ���ȵõ��������������������ߵĶ���M����ABC����ֱ��д��m��ȡֵ��Χ��
����λ������������ƽ��m��m��0������λ���ȵõ��������������������ߵĶ���M����ABC����ֱ��д��m��ȡֵ��Χ��

���𰸡���1��y=![]() x2��x��4����1����
x2��x��4����1����![]() ������2����2����4����6��20������3��0��m��
������2����2����4����6��20������3��0��m��![]() ��
��
�������������������1��ֻ�����ô���ϵ�����Ϳ���������ߵĽ���ʽ��Ȼ�����䷽���Ϳ��������M��������
��2���ɷֵ�P��x����·����Ϸ������������������P��x���·�ʱ�����������ߵ���Գ��Եõ���P������������P��x���Ϸ�ʱ��ֱ��PC��ֱ��ABƽ�������ô���ϵ�������ֱ��AB�Ľ���ʽ��Ȼ���ٸ�����ƽ��ֱ��һ�����ϵ����ͬ�����ֱ��PC�Ľ���ʽ��Ȼ��ֻ�����ֱ��PC�������ߵĽ����������Ϳɽ��������
��3�����������ɵ��������ߵĶ���M����Ϊ��1��m����1�����ʵ�Mʼ����ֱ��y=��1�ϣ���ֱ��y=��1��ֱ��AB���ڵ�P����ֱ��AC���ڵ�Q���ɵ�M�ڡ�ABC�ڿɵõ�M���߶�PQ�ϣ��������˵�P��Q����ֻ�������P��Q���������Ϳɽ�����⣮
���������������1���ߵ�A��0����4����B����2��0����������y=![]() x2+bx+c������
x2+bx+c������![]() �������
������� ![]() ���������ߵĽ���ʽΪy=
���������ߵĽ���ʽΪy=![]() x2��x��4��
x2��x��4��
��y=![]() x2��x��4=
x2��x��4=![]() ��x2��2x+1��1����4=
��x2��2x+1��1����4=![]() ��x��1��2��
��x��1��2��![]() ���������ߵĶ���M������Ϊ��1����
���������ߵĶ���M������Ϊ��1����![]() ����
����
��2���ٵ�P��x����·�����ͼ1��
�ߡ�PCB=��ABC����B���C���ڶԳ���x=1�Գ������A��0����4�����PҲ���ڶԳ���x=1�Գ������P������Ϊ��2����4����
�ڵ�P��x����Ϸ���ֱ��PC��Ϊֱ��l����ͼ2��
��y=0����![]() ��x��1��2��
��x��1��2��![]() =0�������x1=��2��x2=4�����C��������4��0����
=0�������x1=��2��x2=4�����C��������4��0����
��ֱ��AB�Ľ���ʽΪy=kx+t������![]() �������
������� ![]() ����ֱ��AB�Ľ���ʽΪy=��2x��4��
����ֱ��AB�Ľ���ʽΪy=��2x��4��
�ߡ�PCB=��ABC����ֱ��AB��ֱ��l����ֱ��l����Ϊy=��2x+n���ߵ�C��4��0����ֱ��y=��2x+n��������8+n=0����n=8����ֱ��l�Ľ���ʽΪy=��2x+8���ⷽ����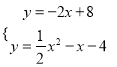 ����
����![]() ��
��![]() �����P����������6��20����
�����P����������6��20����
������������P��������2����4����6��20����
��3��m��ȡֵ��ΧΪ0��m��![]() ��
��
�������������
����ɵ��������߶���M������Ϊ��1��m����![]() +
+![]() ������1��m����1����
������1��m����1����
��ֱ��AC�Ľ���ʽΪy=px+q������![]() �������
������� ![]() ����ֱ��AC�Ľ���ʽΪy=x��4��
����ֱ��AC�Ľ���ʽΪy=x��4��
��ֱ��y=��1��ֱ��AB���ڵ�P����ֱ��AC���ڵ�Q����ͼ3��
�ɩ�2x��4=��1������x=��![]() �����P������Ϊ����
�����P����������![]() ����1����
����1����
��x��4=��1������x=3�����P��������3����1����
���������ߵĶ���M��1��m����1���ڡ�ABC�������M���߶�PQ�ϣ��������˵�P��Q������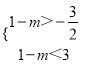 ���������2��m��
���������2��m��![]() ��
��
��m��0����m��ȡֵ��ΧΪ0����m��![]() ��
��


 һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD��CEFG����ͼ���ã���B��C��E��ͬһ��ֱ���ϣ���P��BC���ϣ�PA��PF���ҡ�APF��90�㣬����AF��CD�ڵ�M�������н��ۣ���EC��BP����AP��AM���ۡ�BAP����GFP����AB2��CE2��![]() AF2����S������ABCD��S������CEFG��2S��APF.������ȷ����(����)
AF2����S������ABCD��S������CEFG��2S��APF.������ȷ����(����)
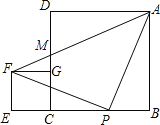
A. �٢ڢ� B. �٢ۢ� C. �٢ڢܢ� D. �٢ۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �Ƶ�A����ʱ�뷽����ת��ʹ��B����BC���ϵĵ�D������
�Ƶ�A����ʱ�뷽����ת��ʹ��B����BC���ϵĵ�D������![]() .��
.��![]() ��
��![]() ����
����![]() �Ķ���.
�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�ͼ���������ĸ�������������ֹ��ɣ���֪��2019Ӧ���ڣ� ��

A. ��505�������ε����Ͻ�B. ��505�������ε����½�
C. ��504�������ε����Ͻ�D. ��504�������ε����½�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
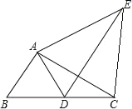
����Ŀ��������ABCD�Ƶ�B˳ʱ����ת�õ�����A1BC1D1����A��C��D�Ķ�Ӧ��ֱ�ΪA1��C1��D1
��1������A1����AC��ʱ
����ͼ1������CAB��60������֤���ı���ABD1CΪƽ���ı��Σ�
����ͼ2��AD1��CB�ڵ�O������CAB��60������֤��DO��AO��
��2����ͼ3����A1D1����Cʱ����BC��5��CD��3��ֱ��д��A1A�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���AB�ij�Ϊ3����E��F�ֱ���AD��BC�ϣ�����BE��DF��EF��BD�����ı���BEDF�����Σ���EF��AE+FC�����BC�ij�Ϊ��������

A. 2![]() B. 3
B. 3![]() C. 6
C. 6![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������2014��1���𣬾���������ˮ��ʼʵ�н���ʽ����ˮ�ۣ��ý���ʽ����ˮ�۷�Ϊ���������±���ʾ����
����ˮ�����֣� | ˮ�ۣ�Ԫ/�֣� |
��һ�� 20�����£���20�֣� | 1.6 |
�ڶ��� 20�֩�30�֣���30�֣� | 2.4 |
������ 30������ | 3.2 |
��1��������û�������ˮ��Ϊ12�֣������ɵ�ˮ��Ϊ Ԫ��
��2��������û��ɵ�ˮ��Ϊ39.2Ԫ����������ˮ�� �֣�
��3��������û�������ˮ��Ϊ![]() �֣�����û�����Ӧ��ˮ�Ѷ���Ԫ�����ú�a�Ĵ���ʽ��ʾ��������
�֣�����û�����Ӧ��ˮ�Ѷ���Ԫ�����ú�a�Ĵ���ʽ��ʾ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒÿ���ɱ�10Ԫ��������ÿ����Ʒ�����ۼ�x��Ԫ�����Ʒ��������y������֮��Ĺ�ϵ���±�����������y�����ۼ�x��һ�κ�����
��1�����������y�����������ۼ�x��Ԫ���ĺ�����ϵʽ��
��2�������۶���Ϊ30Ԫʱ��ÿ�յ���������
x��Ԫ�� | 15 | 20 | 25 | ���� |
y������ | 25 | 20 | 15 | ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ƽ��ֱ������ϵ�У���������![]() ��y��Ľ�����y��Ĵ��ߣ�������������Ǹ������ߵİ���ֱ��.���磺������
��y��Ľ�����y��Ĵ��ߣ�������������Ǹ������ߵİ���ֱ��.���磺������![]() �İ���ֱ��Ϊֱ��
�İ���ֱ��Ϊֱ��![]() .������
.������![]() �İ���ֱ��l��������߽��ڵ�A��D����A��y���ϣ�������������x��Ľ���ΪB(-1,0)��C����C�ڵ�B���Ҳࣩ.
�İ���ֱ��l��������߽��ڵ�A��D����A��y���ϣ�������������x��Ľ���ΪB(-1,0)��C����C�ڵ�B���Ҳࣩ.
��1����ֱ��l��y=2����������߶�Ӧ�ĺ�����ϵʽ.
��2�����D�����꣨�ú�m�Ĵ���ʽ��ʾ��.
��3����������![]() �Ķ���ΪM����OA�Ĵ�ֱƽ����EF����OA�ڵ�E�����������ߵĶԳ����ڵ�F.
�Ķ���ΪM����OA�Ĵ�ֱƽ����EF����OA�ڵ�E�����������ߵĶԳ����ڵ�F.
�ٵ���ADF�ǵ���ֱ��������ʱ�����M������.
�ڽ�ֱ��EF��ֱ��l���۵õ�ֱ��GH������M��ֱ��GH�ľ�����ڵ�C��ֱ��EF�ľ���ʱ��ֱ��д��m��ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com