
【题目】如图,在ABCD中,![]() ,
,![]() ,
,![]() ,点E为CD上一动点,经过A、C、E三点的
,点E为CD上一动点,经过A、C、E三点的![]() 交BC于点F.
交BC于点F.
(操作与发现)
![]() 当E运动到
当E运动到![]() 处,利用直尺与规作出点E与点F;
处,利用直尺与规作出点E与点F;![]() 保留作图痕迹
保留作图痕迹![]()
![]() 在
在![]() 的条件下,证明:
的条件下,证明:![]() .
.
(探索与证明)
![]() 点E运动到任何一个位置时,求证:
点E运动到任何一个位置时,求证:![]() ;
;
(延伸与应用)
![]() 点E在运动的过程中求EF的最小值.
点E在运动的过程中求EF的最小值.

【答案】![]() 作图见解析;
作图见解析;![]() 证明见解析;
证明见解析;![]() 证明见解析;
证明见解析;![]() EF最小值为
EF最小值为![]() .
.
【解析】
![]() 当
当![]() ,此时AC是
,此时AC是![]() 的直径,作出AC的中点O后,以OA为半径作出
的直径,作出AC的中点O后,以OA为半径作出![]() 即可作出点E、F;
即可作出点E、F;
![]() 易知AC为直径,则
易知AC为直径,则![]() ,
,![]() ,从而得证;
,从而得证;
![]() 如图,作
如图,作![]() ,
,![]() ,若E在DN之间,由
,若E在DN之间,由![]() 可知,
可知,![]() ,然后再证明
,然后再证明![]() ∽
∽![]() ,从而可知
,从而可知![]() ,若E在CN之间时,同理可证;
,若E在CN之间时,同理可证;
![]() 由于A、F、C、E四点共圆,所以
由于A、F、C、E四点共圆,所以![]() ,由于四边形ABCD为平行四边形,
,由于四边形ABCD为平行四边形,![]() ,从而可证
,从而可证![]() 为等腰直角三角形,所以
为等腰直角三角形,所以![]() ,由于
,由于![]() ,所以E与N重合时,FE最小.
,所以E与N重合时,FE最小.
![]() 如图1所示,
如图1所示,

![]() 如图,易知AC为直径,则
如图,易知AC为直径,则![]() ,
,
则![]() ,
,
![]() ,
,
![]() 如图,作
如图,作![]() ,
,![]() ,若E在DN之间
,若E在DN之间
由![]() 可知,
可知,![]()
![]() 、F、C、E四点共圆,
、F、C、E四点共圆,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ∽
∽![]()
![]() ,
,
若E在CN之间时,同理可证
![]() 、F、C、E四点共圆,
、F、C、E四点共圆,
![]() ,
,
![]() 四边形ABCD为平行四边形,
四边形ABCD为平行四边形,![]() ,
,

![]() ,
,
![]() ,
,
![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,
,
![]() ,
,
![]() 与N重合时,FE最小,
与N重合时,FE最小,
此时![]() ,
,
在![]() 中,
中,![]() ,则
,则![]()
![]() 由勾股定理可知:
由勾股定理可知:![]()
此时EF最小值为![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发,沿同一路线驶向B地.甲车先出发匀速驶向B地,40min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地.甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法中正确的有( )
①![]() ;②甲的速度是60km/h;③乙出发80min追上甲;④乙刚到达货站时,甲距B地180km.
;②甲的速度是60km/h;③乙出发80min追上甲;④乙刚到达货站时,甲距B地180km.

A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4,E为BC中点,AE⊥BC于点E,AF⊥CD于点F,CG∥AE,CG交AF于点H,交AD于点G.
(1)求菱形ABCD的面积;(2)求∠CHA的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.(1)请用两种不同的方法求图②中阴影部分的面积:
方法1: 方法2:
(2)观察图②请你写出下列三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系. ;
(3)根据(2)题中的等量关系,解决:已知:a﹣b=5,ab=﹣6,求:(a+b)2的值;

查看答案和解析>>
科目:初中数学 来源: 题型:
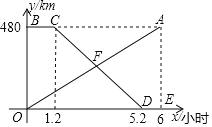
【题目】甲、乙两地相距480km,一辆货车从甲地匀速驶往乙地,货车出发一段时间后,一辆汽车从乙地匀速驶往甲地,设货车行驶的时间为![]() 线段OA表示货车离甲地的距离
线段OA表示货车离甲地的距离![]() 与xh的函数图象;折线BCDE表示汽车距离甲地的距离
与xh的函数图象;折线BCDE表示汽车距离甲地的距离![]() 与
与![]() 的函数图象.
的函数图象.
![]() 求线段OA与线段CD所表示的函数表达式;
求线段OA与线段CD所表示的函数表达式;
![]() 若OA与CD相交于点F,求点F的坐标,并解释点F的实际意义;
若OA与CD相交于点F,求点F的坐标,并解释点F的实际意义;
![]() 当x为何值时,两车相距100千米?
当x为何值时,两车相距100千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.

(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们有时会碰上形如![]() ,
,![]() ,
,![]() 的式子,其实我们可以将其进一步分母有理化.
的式子,其实我们可以将其进一步分母有理化.
形如![]() 的式子还可以用以下方法化简:
的式子还可以用以下方法化简:![]() .(*)
.(*)
(1)请用不同的方法化简(写出化简过程):
(i)参照分母有理化的方法得![]() ______________________________;
______________________________;
(ii)参照(*)式的化简方法得![]() ______________________________.
______________________________.
(2)化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为1cm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B…;依此类推,则平行四边形AO2016C2017B的面积为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com