
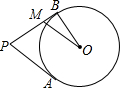
 如图,PA、PB分别与⊙O相切于A、B,点M在PB上,且OM∥AP,若⊙O的半径r=3,PA=9,求OM的长.
如图,PA、PB分别与⊙O相切于A、B,点M在PB上,且OM∥AP,若⊙O的半径r=3,PA=9,求OM的长. 分析 连接OA,作MN⊥AP于N,由切线的性质可知OA⊥AP,OB⊥BP,证得四边形ANMO是矩形,故可得出OA=MN,由OA=MN,OA=OB,OM∥AP.可知OB=MN,∠OMB=∠NPM.故可得出Rt△OBM≌△MNP,OM=MP.设OM=x,则NP=9-x,在Rt△MNP利用勾股定理即可求出x的值,进而得出结论.
解答 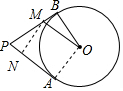 解:连接OA,作MN⊥AP于N
解:连接OA,作MN⊥AP于N
则OA⊥AP,OB⊥BP,
∵MN⊥AP,
∴MN∥OA,
∵OM∥AP,
∴四边形ANMO是矩形,
∴OM=AN,OA=MN
∵OA=OB,OM∥AP.
∴OB=MN,∠OMB=∠NPM,
在△OBM和△MNP中,
$\left\{\begin{array}{l}{∠OMB=∠NPM}\\{∠OBM=∠MNP}\\{OB=MN}\end{array}\right.$.
∴Rt△OBM≌Rt△MNP,
∴OM=MP.
设OM=x,则NP=9-x,
在Rt△MNP中,有x2=32+(9-x)2
∴x=5,即OM=5.
点评 本题考查的是切线的性质、全等三角形的判定与性质、勾股定理及矩形的判定与性质,在解答此类题目时往往连接圆心与切点,构造出直角三角形,再根据直角三角形的性质解答.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
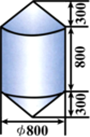 锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是一个圆柱(如图,单位:mm).电镀时,如果每平方米用锌0.11kg,要电镀100个这样的锚标浮筒需要用多少锌?(π取3.14,精确到0.1kg)
锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是一个圆柱(如图,单位:mm).电镀时,如果每平方米用锌0.11kg,要电镀100个这样的锚标浮筒需要用多少锌?(π取3.14,精确到0.1kg)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com