
【题目】如图,在一条不完整的数轴上从左到右有点A,B.将线段AB沿数轴向右移动,移动后的线段记为A′B′,按要求完成下列各小题
(1)若点A为数轴原点,点B表示的数是4,当点A′恰好是AB的中点时,数轴上点B′表示的数为 .
(2)设点A表示的数为m,点A′表示的数为n,当原点在线段A′B之间时,化简|m|+|n|+|m﹣n|.
![]()
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为3的扇形AOB,∠AOB=120°,以AB为边作矩形ABCD交弧AB于点E,F,且点E,F为弧AB的四等分点,矩形ABCD与弧AB形成如图所示的三个阴影区域,其面积分别为![]() ,
,![]() ,
,![]() ,则
,则![]() 为( )(
为( )(![]() 取
取![]() )
)
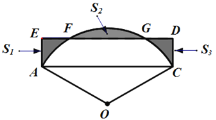
A. ![]()
![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科研所计划建一幢宿舍楼,因为科研所实验中会产生辐射,所以需要有两项配套工程.①在科研所到宿舍楼之间修一条高科技的道路;②对宿含楼进行防辐射处理;已知防辐射费y万元与科研所到宿舍楼的距离xkm之间的关系式为y=ax+b(0≤x≤3).当科研所到宿舍楼的距离为1km时,防辐射费用为720万元;当科研所到宿含楼的距离为3km或大于3km时,辐射影响忽略不计,不进行防辐射处理,设修路的费用与x2成正比,且比例系数为m万元,配套工程费w=防辐射费+修路费.
(1)当科研所到宿舍楼的距离x=3km时,防辐射费y=____万元,a=____,b=____;
(2)若m=90时,求当科研所到宿舍楼的距离为多少km时,配套工程费最少?
(3)如果最低配套工程费不超过675万元,且科研所到宿含楼的距离小于等于3km,求m的范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学分别进行6次射击训练,训练成绩(单位:环)如下表
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六交 | |
甲 | 9 | 8 | 6 | 7 | 8 | 10 |
乙 | 8 | 7 | 9 | 7 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A. 他们训练成绩的平均数相同 B. 他们训练成绩的中位数不同
C. 他们训练成绩的众数不同 D. 他们训练成绩的方差不同
查看答案和解析>>
科目:初中数学 来源: 题型:
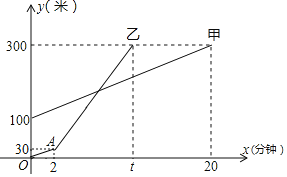
【题目】甲、乙两人相约周末沿同一条路线登山,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题
(1)甲登山的速度是每分钟 米;乙在A地提速时,甲距地面的高度为 米;
(2)若乙提速后,乙的速度是甲登山速度的3倍;
①求乙登山全过程中,登山时距地面的高度y(米)与登山时间x(分钟)之间的函数解析式;
②乙计划在他提速后5分钟内追上甲,请判断乙的计划能实现吗?并说明理由;
(3)当x为多少时,甲、乙两人距地面的高度差为80米?
查看答案和解析>>
科目:初中数学 来源: 题型:
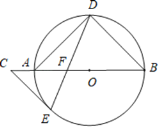
【题目】如图,AB是⊙O的直径,点D,E在⊙O上,∠B=2∠ADE,点C在BA的延长线上.
(Ⅰ)若∠C=∠DAB,求证:CE是⊙O的切线;
(Ⅱ)若OF=2,AF=3,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若用“*”表示一种运算规则,我们规定:a*b=ab﹣a+b,如:3*2=3×2﹣3+2=5.以下说法中错误的是( )
A. 不等式(﹣2)*(3﹣x)<2的解集是x<3
B. 函数y=(x+2)*x的图象与x轴有两个交点
C. 在实数范围内,无论a取何值,代数式a*(a+1)的值总为正数
D. 方程(x﹣2)*3=5的解是x=5
查看答案和解析>>
科目:初中数学 来源: 题型:
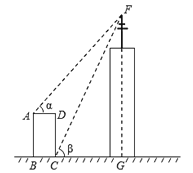
【题目】如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为∠α=48°和∠β=65°,矩形建筑物宽度AD=20m,高度CD=30m,则信号发射塔顶端到地面的高度FG为__米(结果精确到1m).
参考数据:sin48°=0.7,cos48°=0.7,tan48°=1.1,cos65°=0.4,tan65°=2.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com