
【题目】在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.

(1)求反比例函数的表达式;
(2)若![]() 的面积为
的面积为![]() 的面积的2倍,求此直线的函数表达式.
的面积的2倍,求此直线的函数表达式.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)根据题意将点A坐标代入原反比例函数解析式,由此进一步求解即可;
(2)根据题意,将直线解析式![]() 分
分![]() 以及
以及![]() 两种情况结合
两种情况结合![]() 的面积为
的面积为![]() 的面积的2倍进一步分析求解即可.
的面积的2倍进一步分析求解即可.
(1)∵反比例函数![]() (
(![]() )的图象经过点A(3,4),
)的图象经过点A(3,4),
∴![]() ,
,
解得:![]() ,
,
∴原反比例函数解析式为:![]() ;
;
(2)①当直线![]() 的
的![]() 时,函数图像如图所示,
时,函数图像如图所示,
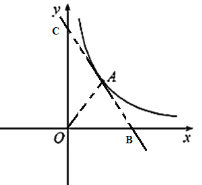
此时![]() ,不符合题意,舍去;
,不符合题意,舍去;
②当直线![]() 的
的![]() 时,函数图像如图所示,
时,函数图像如图所示,
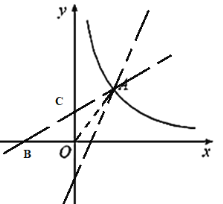
设OC的长度为m,OB的长度为n,
∵![]() 的面积为
的面积为![]() 的面积的2倍
的面积的2倍
∴![]() ,
,
∴![]() ,
,
∴OC的长为2,
∴当C点在y轴正半轴时,点C坐标为(0,2),
∴![]()
∵点A坐标为(3,4),
∴![]() ,
,
∴![]() ,
,
∴直线解析式为:![]() ,
,
当C点在y轴负半轴时,点C坐标为(0,2),
∴![]()
∵点A坐标为(3,4),
∴![]() ,
,
∴![]() ,
,
∴直线解析式为:![]() ,
,
综上所述,直线解析式为:![]() 或
或![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
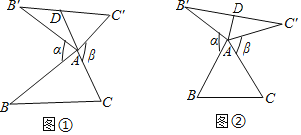
【题目】如图①,在△ABC中,把AB绕点A顺时针旋转α(0°<α<180°)得到AB′,把AC绕点A逆时针旋转β得到AC′,连接B′C′,当α+β=180°时,我们称△AB′C′是△ABC的旋补三角形,△AB′C′边B′C′上的中线AD叫做△ABC的旋补中线.
如图②,当△ABC为等边三角形时,△AB′C′是△ABC的旋补三角形,AD是旋补中线,AD与BC的数量关系为:AD=_____BC;当BC=8时,则B′C′长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
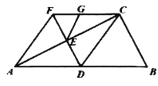
【题目】如图,在![]() 中,
中,![]() 为斜边
为斜边![]() 的中线,过点D作
的中线,过点D作![]() 于点E,延长
于点E,延长![]() 至点F,使
至点F,使![]() ,连接
,连接![]() ,点G在线段
,点G在线段![]() 上,连接
上,连接![]() ,且
,且![]() .下列结论:①
.下列结论:①![]() ;②四边形
;②四边形![]() 是平行四边形;③
是平行四边形;③![]() ;④
;④![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题解答]
两个城镇![]() 与一条公路
与一条公路![]() 位置如图①所示.现电信部门需在公路
位置如图①所示.现电信部门需在公路![]() 上修建一座信号发射塔
上修建一座信号发射塔![]() 要求发射塔
要求发射塔![]() 到两个城镇
到两个城镇![]() 与
与![]() 的距离之和最短.
的距离之和最短.
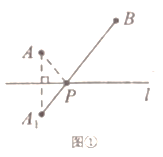
解:点![]() 作关于直线
作关于直线![]() 的对称点
的对称点![]() 连结
连结![]() ,
,
与直线![]() 的交点即为所求的点
的交点即为所求的点![]() .
.
![]() 点
点![]() 关于直线
关于直线![]() 对称,
对称,
![]() 直线
直线![]() 垂直平分
垂直平分![]()
![]()
![]()
![]() 点
点![]() 即为所求的点。(两点之间线段最短)
即为所求的点。(两点之间线段最短)
请根据以上问题解答,完成下列问题.
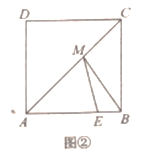
[方法运用]如图②,在正方形![]() 中,
中,![]() 点
点![]() 在边
在边![]() 上,点
上,点![]() 在对角线AC上,
在对角线AC上,
(1)当点![]() 是边
是边![]() 的中点时,则
的中点时,则![]() 的最小值为 ;
的最小值为 ;
(2)若![]() 求
求![]() 周长的最小值.
周长的最小值.
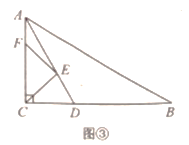
[拓展提升]如图③,在![]() 中,
中,![]() ,AD平分
,AD平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 分别在
分别在![]() 上,则
上,则![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
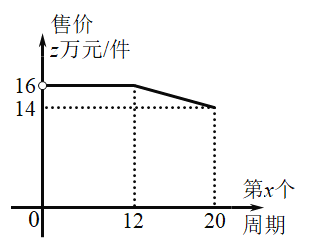
【题目】某工厂计划在每个生产周期内生产并销售完某型设备,设备的生产成本为10万元/件(1)如图,设第x(0<x≤20)个生产周期设备售价z万元/件,z与x之间的关系用图中的函数图象表示,求z关于x的函数解析式(写出x的范围).
(2)设第x个生产周期生产并销售的设备为y件,y与x满足关系式y=5x+40(0<x≤20).在(1)的条件下,工厂在第几个生产周期创造的利润最大?最大为多少万元?(利润=收入-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 的
的![]() 边上取一点
边上取一点![]() ,将
,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 恰好落在
恰好落在![]() 边上点
边上点![]() 处.
处.
(1)如图1,若![]() ,求
,求![]() 的度数;
的度数;
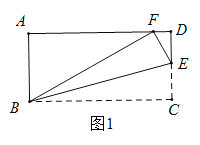
(2)如图2,当![]() ,且
,且![]() 时,求
时,求![]() 的长;
的长;
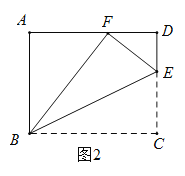
(3)如图3,延长![]() ,与
,与![]() 的角平分线交于点
的角平分线交于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 出的值.
出的值.
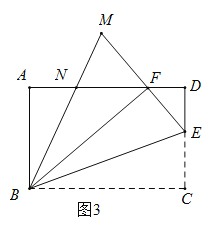
查看答案和解析>>
科目:初中数学 来源: 题型:
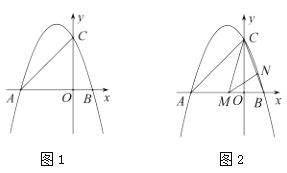
【题目】如图1,抛物线![]() 与两条坐标轴分别交于
与两条坐标轴分别交于![]() ,
,![]() ,
,![]() 三点.其中
三点.其中![]() ,且
,且![]() .
.
(1)求该抛物线的解析式;
(2)点![]() 是
是![]() 轴上一点,抛物线上是否存在点
轴上一点,抛物线上是否存在点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点,以
为顶点,以![]() 为边的四边形是平行四边形?若存在,求出点
为边的四边形是平行四边形?若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)如图2,点![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 上的动点,连接
上的动点,连接![]() ,
,![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 在
在![]() 上.则下列命题为真命题的是( )
上.则下列命题为真命题的是( )
A.若半径![]() 平分弦
平分弦![]() .则四边形
.则四边形![]() 是平行四边形
是平行四边形
B.若四边形![]() 是平行四边形.则
是平行四边形.则![]()
C.若![]() .则弦
.则弦![]() 平分半径
平分半径![]()
D.若弦![]() 平分半径
平分半径![]() .则半径
.则半径![]() 平分弦
平分弦![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数y=![]() (x>0)的图象与直线y=mx交于点A(2,2).
(x>0)的图象与直线y=mx交于点A(2,2).
(1)求k,m的值;
(2)点P的横坐标为n(n>0),且在直线y=mx上,过点P作平行于x轴的直线,交y轴于点M,交函数y=![]() (x>0)的图象于点N.
(x>0)的图象于点N.
①n=1时,用等式表示线段PM与PN的数量关系,并说明理由;
②若PN≥3PM,结合函数的图象,直接写出n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com