
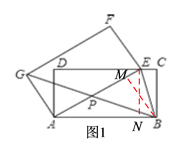
【题目】如图,将矩形ABCD绕点A按逆时针方向旋转,得到矩形AEFG,E点正好落在边CD上,连接BE,BG,且BG交AE于P.
(1)求证:∠CBE=![]() ∠BAE;
∠BAE;
(2)求证:PG=PB;
(3)若AB=![]() ,BC=3,求出BG的长.
,BC=3,求出BG的长.

【答案】(3)![]()
【解析】试题分析:
(1)由已知条件易得AE=AB,由此可得∠BAE=180°-2∠ABE,结合∠CBE=90°-∠ABE即可得到∠CBE=![]() ∠BAE;
∠BAE;
(2)如图1,过点B作BM⊥AE于点M,过点E作EN⊥AB于点N,由AE=BE,易得BM=EN=BC=GA,再证△PBM≌△PGA即可得到PG=PB;
(3)如图1,BM=BC=3,结合AB=![]() 在Rt△ABM中由勾股定理可得AM=
在Rt△ABM中由勾股定理可得AM=![]() ,由(2)中△PBM≌△PGA可得PM=AP=
,由(2)中△PBM≌△PGA可得PM=AP=![]() AM=
AM=![]() ,由此在Rt△PBM中可得PB=
,由此在Rt△PBM中可得PB=![]() 结合(2)中结论PB=PG即可得到BG=2PB=
结合(2)中结论PB=PG即可得到BG=2PB=![]() .
.
试题解析:
(1)∵矩形AEFG是由矩形ABCD绕点A旋转得到的,
∴AE=AB,∠ABC=90°,
∴∠ABE=∠AEB,
∴∠BAE=180°-2∠ABE,
∵∠CBE=90°-∠ABE,
∴∠CBE=![]() ∠BAE;
∠BAE;
(2)如图1,过点B作BM⊥AE于点M,过点E作EN⊥AB于点N,
∴S△ABE=![]() AB·EN=
AB·EN=![]() AE·BM,
AE·BM,
∵AE=AB,
∴BM=EN=BC=GA,
∵矩形AEFG是由矩形ABCD绕点A旋转得到的,
∴∠BMA=∠ENB=∠ABC=∠C=∠GAE=90°,GA=EF=BC,
∴四边形ENBC是矩形,
∴EN=BC=GA,
∴BM=GA,
又∵∠APG=∠MPB,
∴△PBM≌△PGA,
∴PG=PB;
(3)如图1,∵BM=BC=3,∠AMB=90°,AB=![]() ,
,
∴AM=![]() ,
,
∵△PBM≌△PGA,
∴PM=PA=![]() ,
,
∴在Rt△PBM中,PB=![]() ,
,
又∵PB=PG,
∴BG=![]() .
.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,反映的是某中学九(3)班学生外出方式(乘车、步行、骑车)的频数(人数)分布直方图(部分)和扇形分布图,那么下列说法正确的是( )
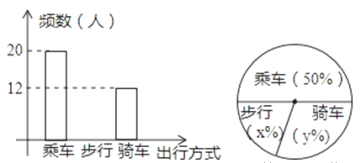
A. 九(3)班外出的学生共有42人
B. 九(3)班外出步行的学生有8人
C. 在扇形图中,步行的学生人数所占的圆心角为82°
D. 如果该校九年级外出的学生共有500人,那么估计全年级外出骑车的学生约有140人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,点E.F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF、则EF=BE+DF,试说明理由;
(2)类比引申
如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E.F分别在边BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF;
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD、DE、EC满足的等量关系,并写出推理过程。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上,则a的值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为______cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠A=60°,点D是BC边的中点,作射线DE,与边AB交于点E,射线DE绕点D顺时针旋转120°,与直线AC交于点F.
(1)依题意将图1补全;
(2)小华通过观察、实验提出猜想:在点E运动的过程中,始终有DE=DF.小华把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:由点D是BC边的中点,通过构造一边的平行线,利用全等三角形,可证DE=DF;
想法2:利用等边三角形的对称性,作点E关于线段AD的对称点P,由∠BAC与∠EDF互补,可得∠AED与∠AFD互补,由等角对等边,可证DE=DF;
想法3:由等腰三角形三线合一,可得AD是∠BAC的角平分线,由角平分线定理,构造点D到AB,AC的高,利用全等三角形,可证DE=DF….
请你参考上面的想法,帮助小华证明DE=DF(选一种方法即可);
(3)在点E运动的过程中,直接写出BE,CF,AB之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)求每个篮球和每个足球的售价;
(2)如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com