
����Ŀ��Ϊ�˽�һ���˽���꼶ѧ�����������������������ʦ���꼶��1����50λѧ������һ���������������ԣ��Բ�������Ϊ���������Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��������ʾ��
��� | ����x | Ƶ���������� |
��1�� | 80��x��100 | 6 |
��2�� | 100��x��120 | 8 |
��3�� | 120��x��140 | a |
��4�� | 140��x��160 | 18 |
��5�� | 160��x��180 | 6 |
����ͼ������������⣺
��1�����е�a= ��
��2�����Ƶ���ֲ�ֱ��ͼ����������
��3������������ݵ���λ�����ڵ� �飻
��4�������꼶ѧ��һ��������������x�����Ҫ���ǣ�x��120���ϸ�120��x��140Ϊ�ϸ�140��x��160Ϊ����x��160Ϊ�ţ�����������Ϣ�������ѧУ����꼶ͬѧ��һ�����������飺 ��

���𰸡���1��a=12����2����ͼ�μ���������3�����ڵ����飻��4��Ҫ��80��100������6�˶�������𰸲�Ψһ����
��������
�����������1������ֱ��ͼ�����壬����Ƶ��֮�ͼ������������������ֻ��������������Ƶ������a��ֵ����2�����ݣ�1���Ĵ𰸣���ȫֱ��ͼ���ɣ���3��������λ�������Ƚ����ݰ���С�����˳�����У��м�λ�õ��Ǹ������м����������ƽ����������λ������ͼ�пɿ�������λ�������ڵ�λ�ã���4���������⣬���ͳ�Ʊ�����Ϣ�����������Ľ��鼴�ɣ�
�����������1����������������������Ƶ����a=50��6��8��18��6=12����2�����ݣ�1���Ĵ𰸣���ȫֱ��ͼ��ͼ��ʾ��
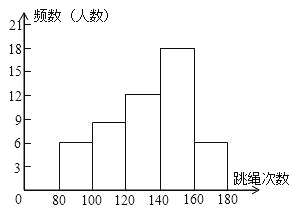
��3��������λ�������Ƚ����ݰ���С�����˳�����У���ͼ�ɵã���50�ˣ���25��26�����ڵ�3�飬
��������������ݵ���λ�����ڵ����飻��4������ֱ��ͼ����Ϣ�����������Ľ��飬�𰸲�Ψһ����Ҫ��80��100������6�˶������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
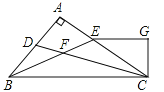
����Ŀ����ͼ����ABC�Ľ�ƽ���� CD��BE�ཻ��F����A=90����EG��BC����CG��EG��G�����н��ۣ��١�CEG=2��DCB����CAƽ�֡�BCG���ۡ�ADC=��GCD���ܡ�DFB=![]() ��CGE��
��CGE��
������ȷ�Ľ�����_____________������ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��EF�����A����C����D����E�����������ϵ�ǣ� ��

A. ��A����C����D����E��360��
B. ��A����D����C����E
C. ��A����C����D����E��180��
D. ��E����C����D����A��90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���й�·l1ͬ�ࡢl2������������A��B�����Ų���Ҫ��S����һ���źŷ��������������Ҫ����������������A��B�ľ��������ȣ���������·l1��l2�ľ���Ҳ������ȣ�������CӦ����ʲôλ�ã����ó߹���ͼ�ҳ����з��������ĵ㣬ע����C��λ�ã�(������ͼ�ۼ�����д����)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
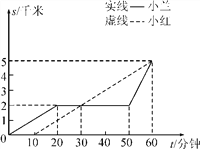
����Ŀ��С����С����ѧУ��������ѧУ5ǧ��������飬��ͼ��Ӧ�����������뿪ѧУ��·����ʱ��Ĺ�ϵ�������ͼ�ν�����⣮
(1)С����С��˭�ȳ���������������ӣ�
(2)С��ǰ20���ӵ��ٶȺ����10���ӵ��ٶȸ��Ƕ��٣�
(3)С����С����ѧУ������ƽ���ٶȸ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����AB=BC=AC=12cm����������M��N�ֱ�ӵ�A����Bͬʱ�������������εı��˶�����֪��M���ٶ�Ϊ1cm/s����N���ٶ�Ϊ2cm/s������N��һ�ε���B��ʱ��M��Nͬʱֹͣ�˶���

��1����M��N�˶��������M��N�����غϣ�
��2����M��N�˶���������ɵõ��ȱ���������AMN��
��3������M��N��BC�����˶�ʱ���ܷ�õ���MNΪ�ױߵĵ��������Σ���������������ʱM��N�˶���ʱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ����������ʵʩ����ͬ��һ�廯�����̽�չ˳������Ͷ�������ڶԹ۹�·�����б�ʱ���ӵ��ס����������̶ӵ�Ͷ���飬�ס���ʩ��һ��Ĺ��̷��÷ֱ�Ϊ1.5��Ԫ��1.1��Ԫ������Ͷ�����ĸ��ݼ��������ӵ�Ͷ������㣬Ӧ������ʩ��������
��1���ӵ���������̸պ�������ɣ�
��2���Ҷӵ���������̣�Ҫ�ȹ涨���ڶ�5�죻
��3�����ס������Ӻ���4������µĹ������Ҷӵ�������Ҳ����������ɣ�
��ȷ��������ɵ�����£�����Ϊ���ַ������ʡ���̿ͨ������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
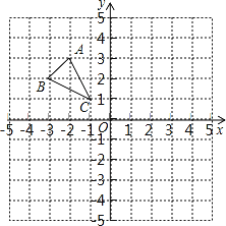
����Ŀ����ͼ����ABC�Ķ���ֱ�ΪA��-2,3����B��-3,2����C��-1,1��
��1��������ABC����y��ԳƵġ�A1B1C1��
��2������x����ȷ��һ��D��ʹ��D��B��C�ľ�����ȣ�Ҫ����ֱ�ߺ�Բ����ͼ����������ͼ�ۼ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�������Σ���EBC�ǵȱ������Σ�
��1����֤����ABE�ա�DCE��
��2������AED�Ķ�����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com