
分析 (1)先根据乘法公式计算,然后合并同类二次根式即可;
(2)先化简二次根式,合并二次根式,再根据乘法计算方法计算即可;
(3)根据题意求得x的值,代入$\sqrt{{x}^{2}-2x+1}$+$\sqrt{3x-1}$计算即可.
解答 解:(1)原式=3-2-(3-2$\sqrt{2}$)
=2$\sqrt{2}$-2.
(2)原式=2$\sqrt{3}$(2$\sqrt{3}$-15$\sqrt{3}$+2$\sqrt{3}$)
=-2$\sqrt{3}$•11$\sqrt{3}$
=-66.
(3)由题意可知:6≤x<9,且x为奇数,则x=7,
$\sqrt{{x}^{2}-2x+1}$+$\sqrt{3x-1}$=6+2$\sqrt{5}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{0.34}$ | B. | $\sqrt{\frac{2}{5}}$ | C. | $\sqrt{{a}^{2}+1}$ | D. | $\sqrt{7a{b}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
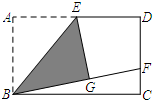 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=2,FD=4,则BC的长为( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=2,FD=4,则BC的长为( )| A. | 6$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{5}$ | D. | 4$\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com