
分析 把分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)方程两边乘以(x+2)(x-2)得:x-2+4x=2(x+2),
解得:x=2,
检验:x=2时,(x+2)(x-2)=0,x=2不是原方程的解:
因此,原方程无解.
(2)方程两边乘以2(x-1)得:3-2=6(x-1),
解得:x=$\frac{7}{6}$,
检验:x=$\frac{7}{6}$时,2(x-1)≠0,x=$\frac{7}{6}$是原方程的解:
因此,原方程的解为x=$\frac{7}{6}$.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.


科目:初中数学 来源: 题型:选择题
| A. | x>$\frac{4}{3}$ | B. | x>$\frac{3}{4}$ | C. | x$≥\frac{3}{4}$ | D. | x≥$\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2、6) | B. | (2、-6) | C. | (4、-3) | D. | (3、-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
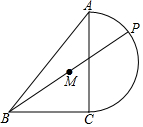 如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )
如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )| A. | 2$\sqrt{2}$π | B. | $\sqrt{2}$π | C. | 2π | D. | 2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com