
 如图,在菱形ABCD中,∠BAD=60°,M为对角线BD延长线上一点,连接AM和CM,E为CM上一点,且满足CB=CE,连接BE,交CD于点F.
如图,在菱形ABCD中,∠BAD=60°,M为对角线BD延长线上一点,连接AM和CM,E为CM上一点,且满足CB=CE,连接BE,交CD于点F.分析 (1)首先证明∠MAB=90°,再证明△BMA≌△BMC,推出∠BCE=90°,利用勾股定理即可解决问题.
(2)如图2中,在BD上取一点G,使得BG=DF,连接CG交BE于O.只要证明△GBC≌△FDB,MG=MC即可解决问题.
解答 (1)解:如图1中,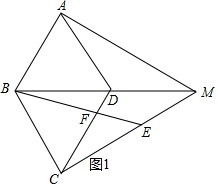
∵四边形ABCD是菱形,∠BAD=60°,
∴△ABD,△BCD的是等边三角形,
∴∠ABD=∠CBD=∠ADB=∠BAD=60°,BA=BC,
∵∠AMB=30°,∠ADB=∠AMB+∠DAM,
∴∠DAM=∠DMA=30°,
∴∠BAM=90°,DA=DM=AB=BC=CE=3,
在△BMA和△BMC中,
$\left\{\begin{array}{l}{BM=BM}\\{∠MBA=∠MBC}\\{BA=BC}\end{array}\right.$,
∴△BMA≌△BMC,
∴∠BCM=∠BAM=90°,
在Rt△BCE中,BE=$\sqrt{B{C}^{2}+C{E}^{2}}$=3$\sqrt{2}$.
(2)如图2中,在BD上取一点G,使得BG=DF,连接CG交BE于O.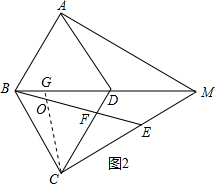
∵BG=DF,∠CBG=∠BDF,BD=BC,
∴△GBC≌△FDB,
∴∠BGC=∠BFD,∠DBF=∠BCG,
∴∠MGC=∠BFC,
∵∠COF=∠CBO+∠OCB=∠CBO+∠DBF=60°
在△COE中,∠ECO+∠EOC+∠CEO=180°,
在△BCF中,∠BFC+∠CBF+∠BCF=180°,
∵CB=CE,
∴∠CBE=∠CEO,∵∠BCF=∠COE=60°,
∴∠ECO=∠BFC=∠MGC,
∴MC=MG,
由(1)可知△BMA≌△BMC,
∴AM=MC=MG,
∵MG=DG+DM,
∵BD=CD,BG=DF,
∴DG=CF,
∴AM=CF+DM
点评 本题考查菱形的性质、等边三角形的性质、全等三角形的判定和性质、勾股定理、等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线(截长补短法),构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
 为积极响应沙坪坝区创建全国文明城区活动,某校举行了以“弘扬社会主义核心价值观”为主题的征文比赛,校德育处对全校每班的投稿篇数进行了统计,并绘制了如图所示条形统计图,则在本次征文比赛中,平均每班投稿篇数为8.
为积极响应沙坪坝区创建全国文明城区活动,某校举行了以“弘扬社会主义核心价值观”为主题的征文比赛,校德育处对全校每班的投稿篇数进行了统计,并绘制了如图所示条形统计图,则在本次征文比赛中,平均每班投稿篇数为8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
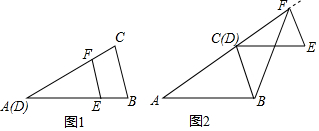
| A. | △DEF平移的距离是m | B. | 图2中,CB平分∠ACE | ||
| C. | △DEF平移的距离是n | D. | 图2中,EF∥BC |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点E在AC的延长线上,已知AB∥CD,对于给出的四个结论:(1)∠1=∠2;(2)∠3=∠4;(3)∠A=∠DCE;(4)∠D+∠ABD=180°,正确的有3个.
如图,点E在AC的延长线上,已知AB∥CD,对于给出的四个结论:(1)∠1=∠2;(2)∠3=∠4;(3)∠A=∠DCE;(4)∠D+∠ABD=180°,正确的有3个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com