
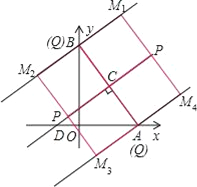
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖRt”÷AOBµÄĮ½Ö±½Ē±ßOA”¢OB·Ö±šŌŚxÖį”¢yÖįµÄÕż°ėÖįÉĻ£ØOA£¼OB£©£¬ĒŅOA”¢OBµÄ³¤·Ö±šŹĒŅ»ŌŖ¶ž“Ī·½³Ģx2©14x+48=0µÄĮ½øöøł£®Ļ߶ĪABµÄ“¹Ö±Ę½·ÖĻßCD½»ABÓŚµćC£¬½»xÖįÓŚµćD£¬µćPŹĒÖ±ĻßCDÉĻŅ»øö¶Æµć£¬µćQŹĒÖ±ĻßABÉĻŅ»øö¶Æµć£®
£Ø1£©ĒóA”¢BĮ½µćµÄ×ų±ź£»
£Ø2£©ĒóÖ±ĻßCDµÄ½āĪöŹ½£»
£Ø3£©ŌŚ×ų±źĘ½ĆęÄŚŹĒ·ń“ęŌŚµćM£¬Ź¹ŅŌµćC”¢P”¢Q”¢MĪŖ¶„µćµÄĖıߊĪŹĒÕż·½ŠĪ£¬ĒŅøĆÕż·½ŠĪµÄ±ß³¤ĪŖ![]() AB³¤£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćMµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
AB³¤£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćMµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

”¾“š°ø”æ£Ø1£©A£Ø6£¬0£©£¬B£Ø0£¬8£©£»
£Ø2£©y=![]() x+
x+![]() £»
£»
£Ø3£©“ęŌŚ£¬M1£Ø4£¬11£©£¬M2£Ø©4£¬5£©£¬M3£Ø2£¬©3£©£¬M4£Ø10£¬3£©
”¾½āĪö”放ŹŌĢā·ÖĪö”æ£Ø1£©ĄūÓĆŅņŹ½·Ö½ā·Ø½ā·½³Ģx2©14x+48=0£¬Ēó³öxµÄÖµ£¬¼“æɵƵ½A”¢BĮ½µćµÄ×ų±ź£»
£Ø2£©ĻČŌŚRt”÷AOBÖŠĄūÓĆ¹“¹É¶ØĄķĒó³öAB=![]() =10£¬øł¾ŻĻ߶Ī“¹Ö±Ę½·ÖĻߵĊŌÖŹµĆµ½AC=
=10£¬øł¾ŻĻ߶Ī“¹Ö±Ę½·ÖĻߵĊŌÖŹµĆµ½AC=![]() AB=5£®ŌŁÓÉĮ½½Ē¶ŌÓ¦ĻąµČµÄĮ½Čż½ĒŠĪĻąĖĘÖ¤Ć÷”÷ACD”×”÷AOB£¬ÓÉĻąĖĘČż½ĒŠĪ¶ŌÓ¦±ß³É±ČĄżµĆ³ö
AB=5£®ŌŁÓÉĮ½½Ē¶ŌÓ¦ĻąµČµÄĮ½Čż½ĒŠĪĻąĖĘÖ¤Ć÷”÷ACD”×”÷AOB£¬ÓÉĻąĖĘČż½ĒŠĪ¶ŌÓ¦±ß³É±ČĄżµĆ³ö![]() £¬Ēó³öAD=
£¬Ēó³öAD=![]() £¬µĆµ½Dµć×ų±ź£Ø©
£¬µĆµ½Dµć×ų±ź£Ø©![]() £¬0£©£¬øł¾ŻÖŠµć×ų±ź¹«Ź½µĆ³öC£Ø3£¬4£©£¬Č»ŗóĄūÓĆ“ż¶ØĻµŹż·Ø¼“æÉĒó³öÖ±ĻßCDµÄ½āĪöŹ½£»
£¬0£©£¬øł¾ŻÖŠµć×ų±ź¹«Ź½µĆ³öC£Ø3£¬4£©£¬Č»ŗóĄūÓĆ“ż¶ØĻµŹż·Ø¼“æÉĒó³öÖ±ĻßCDµÄ½āĪöŹ½£»
£Ø3£©·ÖĮ½ÖÖĒéæö½ųŠŠĢÖĀŪ£ŗ¢Łµ±µćQÓėµćBÖŲŗĻŹ±£¬ĻČĒó³öBMµÄ½āĪöŹ½ĪŖy=![]() x+8£¬ÉčM£Øx£¬
x+8£¬ÉčM£Øx£¬ ![]() x+8£©£¬ŌŁøł¾ŻBM=5ĮŠ³ö·½³Ģ£Ø
x+8£©£¬ŌŁøł¾ŻBM=5ĮŠ³ö·½³Ģ£Ø![]() x+8©8£©2+x2=52£¬½ā·½³Ģ¼“æÉĒó³öMµÄ×ų±ź£»¢Śµ±µćQÓėµćAÖŲŗĻŹ±£¬ĻČĒó³öAMµÄ½āĪöŹ½ĪŖy=
x+8©8£©2+x2=52£¬½ā·½³Ģ¼“æÉĒó³öMµÄ×ų±ź£»¢Śµ±µćQÓėµćAÖŲŗĻŹ±£¬ĻČĒó³öAMµÄ½āĪöŹ½ĪŖy=![]() x©
x©![]() £¬ÉčM£Øx£¬
£¬ÉčM£Øx£¬ ![]() x©
x©![]() £©£¬ŌŁøł¾ŻAM=5ĮŠ³ö·½³Ģ£Ø
£©£¬ŌŁøł¾ŻAM=5ĮŠ³ö·½³Ģ£Ø![]() x©
x©![]() £©2+£Øx©6£©2=52£¬½ā·½³Ģ¼“æÉĒó³öMµÄ×ų±ź£®
£©2+£Øx©6£©2=52£¬½ā·½³Ģ¼“æÉĒó³öMµÄ×ų±ź£®
”¾ŹŌĢā½āĪö”æ
£Ø1£©½ā·½³Ģx2©14x+48=0£¬
µĆx1=6£¬x2=8£¬
”ßOA£¼OB£¬
”ąA£Ø6£¬0£©£¬B£Ø0£¬8£©£»
£Ø2£©ŌŚRt”÷AOBÖŠ£¬”ß”ĻAOB=90”ć£¬OA=6£¬OB=8£¬
”ąAB=![]() =10£¬
=10£¬
”ßĻ߶ĪABµÄ“¹Ö±Ę½·ÖĻßCD½»ABÓŚµćC£¬
”ąAC=![]() AB=5£®
AB=5£®
ŌŚ”÷ACDÓė”÷AOBÖŠ£¬
![]() £¬
£¬
”ą”÷ACD”×”÷AOB£¬
”ą![]() £¬¼“
£¬¼“![]() £¬
£¬
½āµĆAD=![]() £¬
£¬
”ßA£Ø6£¬0£©£¬µćDŌŚxÖįÉĻ£¬
”ąD£Ø©![]() £¬0£©£®
£¬0£©£®
ÉčÖ±ĻßCDµÄ½āĪöŹ½ĪŖy=kx+b£¬
ÓÉĢāŅāÖŖCĪŖABÖŠµć£¬
”ąC£Ø3£¬4£©£¬
”ßD£Ø©![]() £¬0£©£¬
£¬0£©£¬
”ą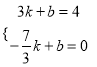 £¬½āµĆ
£¬½āµĆ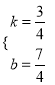 £¬
£¬
”ąÖ±ĻßCDµÄ½āĪöŹ½ĪŖy=![]() x+
x+![]() £»
£»
£Ø3£©ŌŚ×ų±źĘ½ĆęÄŚ“ęŌŚµćM£¬Ź¹ŅŌµćC”¢P”¢Q”¢MĪŖ¶„µćµÄĖıߊĪŹĒÕż·½ŠĪ£¬ĒŅøĆÕż·½ŠĪµÄ±ß³¤ĪŖ![]() AB³¤£®
AB³¤£®
”ßAC=BC=![]() AB=5£¬
AB=5£¬
”ąŅŌµćC”¢P”¢Q”¢MĪŖ¶„µćµÄÕż·½ŠĪµÄ±ß³¤ĪŖ5£¬ĒŅµćQÓėµćB»ņµćAÖŲŗĻ£®·ÖĮ½ÖÖĒéæö£ŗ
µ±µćQÓėµćBÖŲŗĻŹ±£¬Ņ×ĒóBMµÄ½āĪöŹ½ĪŖy=![]() x+8£¬ÉčM£Øx£¬
x+8£¬ÉčM£Øx£¬ ![]() x+8£©£¬
x+8£©£¬
”ßB£Ø0£¬8£©£¬BM=5£¬
”ą£Ø![]() x+8©8£©2+x2=52£¬
x+8©8£©2+x2=52£¬
»Æ¼ņÕūĄķ£¬µĆx2=16£¬
½āµĆx=”Ą4£¬
”ąM1£Ø4£¬11£©£¬M2£Ø©4£¬5£©£»
µ±µćQÓėµćAÖŲŗĻŹ±£¬Ņ×ĒóAMµÄ½āĪöŹ½ĪŖy=![]() x©
x©![]() £¬ÉčM£Øx£¬
£¬ÉčM£Øx£¬ ![]() x©
x©![]() £©£¬
£©£¬
”ßA£Ø6£¬0£©£¬AM=5£¬
”ą£Ø![]() x©
x©![]() £©2+£Øx©6£©2=52£¬
£©2+£Øx©6£©2=52£¬
»Æ¼ņÕūĄķ£¬µĆx2©12x+20=0£¬
½āµĆx1=2£¬x2=10£¬
”ąM3£Ø2£¬©3£©£¬M4£Ø10£¬3£©£»
×ŪÉĻĖłŹö£¬ĖłĒóµćMµÄ×ų±źĪŖM1£Ø4£¬11£©£¬M2£Ø©4£¬5£©£¬M3£Ø2£¬©3£©£¬M4£Ø10£¬3£©£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŅʶÆĶØѶ¹«Ė¾Ģį¹©ĮĖA£¬BĮ½ÖÖ·½°øµÄĶØѶ·ŃÓĆy(ŌŖ)ÓėĶØ»°Ź±¼äx(·Ö)Ö®¼äµÄ¹ŲĻµ£¬ČēĶ¼ĖłŹ¾£¬ŌņŅŌĻĀĖµ·Ø“ķĪóµÄŹĒ( )
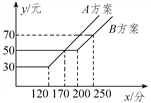
A. ČōĶØ»°Ź±¼äÉŁÓŚ120·Ö£¬ŌņA·½°ø±ČB·½°ø±ćŅĖ20ŌŖ
B. ČōĶØ»°Ź±¼ä³¬¹ż200·Ö£¬ŌņB·½°ø±ČA·½°ø±ćŅĖ12ŌŖ
C. ČōĶØѶ·ŃÓĆĪŖ60ŌŖ£¬ŌņB·½°ø±ČA·½°øµÄĶØ»°Ź±¼ä¶ą
D. ČōĮ½ÖÖ·½°øĶØѶ·ŃÓĆĻą²ī10ŌŖ£¬ŌņĶØ»°Ź±¼äŹĒ145·Ö»ņ185·Ö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÖŠ£¬AB£½AC£¬ŅŌABĪŖÖ±¾¶µÄ”ŃO·Ö±šÓėBC”¢AC½»ÓŚµćD”¢E£¬¹żµćD×÷”ŃOµÄĒŠĻßDF£¬½»ACÓŚµćF£®
£Ø1£©ĒóÖ¤£ŗDF”ĶAC£»
£Ø2£©Čō”ŃOµÄ°ė¾¶ĪŖ4£¬”ĻCDF£½22.5”ć£¬ĒóŅõÓ°²æ·ÖµÄĆ껿£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»“ĪŗÆŹży£½kx£«bÓė·“±ČĄżŗÆŹży£½![]() £Øx£¾0£©½»ÓŚA£Ø2£¬4£©£¬B£Øa£¬1£©£¬ÓėxÖį£¬yÖį·Ö±š½»ÓŚµćC£¬D£®
£Øx£¾0£©½»ÓŚA£Ø2£¬4£©£¬B£Øa£¬1£©£¬ÓėxÖį£¬yÖį·Ö±š½»ÓŚµćC£¬D£®
£Ø1£©Ö±½ÓŠ“³öŅ»“ĪŗÆŹży£½kx£«bµÄ±ķ“ļŹ½ŗĶ·“±ČĄżŗÆŹży£½![]() £Øx£¾0£©µÄ±ķ“ļŹ½£»
£Øx£¾0£©µÄ±ķ“ļŹ½£»
£Ø2£©ĒóÖ¤£ŗAD£½BC£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ADŹĒ”÷ABCµÄÖŠĻߣ¬E£¬F·Ö±šŹĒADŗĶADŃÓ³¤ĻßÉĻµÄµć£¬ĒŅDE=DF£¬Į¬½įBF£¬CE£®ĻĀĮŠĖµ·Ø£ŗ
¢Ł”÷ABDŗĶ”÷ACDĆ껿ĻąµČ£»
¢Ś”ĻBAD=”ĻCAD£»
¢Ū”÷BDF”Õ”÷CDE£»
¢ÜBF”ĪCE£»
¢ŻCE£½AE£®
ĘäÖŠÕżČ·µÄÓŠ£Ø £©

A£®1øö B£®2øö C£®3øö D£®4øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
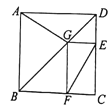
”¾ĢāÄæ”æČēĶ¼ĪŖij³ĒŹŠ²æ·Ö½ÖµĄŹ¾ŅāĶ¼£¬ĖıߊĪABCDĪŖÕż·½ŠĪ£¬µćGŌŚ¶Ō½ĒĻßBDÉĻ£¬GE”ĶCD£¬GF”ĶBC£¬AD=1500m£¬Š”ĆōŠŠ×ßµÄĀ·ĻßĪŖB”śA”śG”śE£¬Š”“ĻŠŠ×ßµÄĀ·ĻßĪŖB”śA”śD”śE”śF£®ČōŠ”ĆōŠŠ×ßµÄĀ·³ĢĪŖ3100m£¬ŌņŠ”“ĻŠŠ×ßµÄĀ·³ĢĪŖ m£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖÕż·½ŠĪ¢Ł”¢¢ŚŌŚÖ±ĻßÉĻ£¬Õż·½ŠĪ¢ŪČēĶ¼·ÅÖĆ£¬ČōÕż·½ŠĪ¢Ł”¢¢ŚµÄĆ껿·Ö±šĪŖ81 cm2ŗĶ144 cm2£¬ŌņÕż·½ŠĪ¢ŪµÄ±ß³¤ĪŖ£Ø””””£©

A. 225 cm B. 63 cm C. 50 cm D. 15 cm
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪABCDÖŠ£¬¶Ō½ĒĻßAC,BDĻą½»ÓŚOµć£¬µćPŹĒĻ߶ĪADÉĻŅ»¶Æµć£Ø²»ÓėµćDÖŲŗĻ£©£¬POµÄŃÓ³¤Ļß½»BCÓŚQµć£®
£Ø1£©ĒóÖ¤£ŗĖıߊĪPBQDĪŖĘ½ŠŠĖıߊĪ.
£Ø2£©ČōAB=3cm£¬AD=4cm£¬P“ÓµćA³ö·¢£®ŅŌ1cm/sµÄĖŁ¶ČĻņµćDŌČĖŁŌĖ¶Æ£®ÉčµćPµÄŌĖ¶ÆŹ±¼äĪŖts£¬ĪŹ£ŗĖıߊĪPBQDÄܹ»³ÉĪŖĮāŠĪĀš£æČē¹ūÄÜ£¬Ēó³öĻąÓ¦µÄtÖµ£»Čē¹ū²»ÄÜ£¬ĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC=1£¬BC=![]() £¬ŌŚAC±ßÉĻ½ŲČ”AD=BC£¬Į¬½ÓBD£®
£¬ŌŚAC±ßÉĻ½ŲČ”AD=BC£¬Į¬½ÓBD£®
£Ø1£©Ķعż¼ĘĖć£¬ÅŠ¶ĻAD2ÓėACCDµÄ“󊔹ŲĻµ£»
£Ø2£©Ēó”ĻABDµÄ¶ČŹż£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com