
在线段AB上取一个点,图中线段的总数S1=3;
在线段AB上取两个点,图中线段的总数S2=6;
在线段AB上取三个点,图中线段的总数S3=10.
![]()
则S1=3=1+2;
S2=6=1+2+3;
S3=10=1+2+3+4;
…
照此规律,在线段AB上取9个点,则图中线段的总数为:
S9=1+2+3+…+9+10=55.
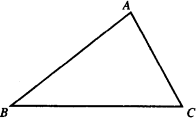
采用类比的方法,在三角形BC边上取9个点,把这些点与A点分别联结起来.问图中共有多少个三角形?
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
| 5 |
| 2 |
| 13 |
| 4 |
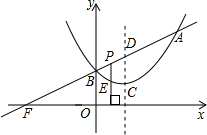 三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
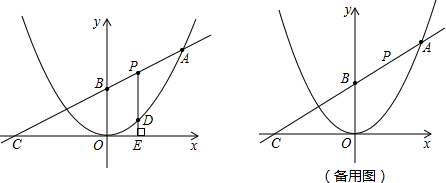
 OC相似?若存在,请求出P点的坐标;若不存在,请说明理由.
OC相似?若存在,请求出P点的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com