
 如图所示,在?ABCD中,平行于对角线AC的直线MN分别交DA,DC的延长线于点M,N,交BA,BC于点P,Q.求证:MP=QN.
如图所示,在?ABCD中,平行于对角线AC的直线MN分别交DA,DC的延长线于点M,N,交BA,BC于点P,Q.求证:MP=QN.  口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:填空题
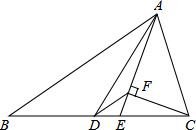 如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则$\frac{AF}{EF}$=$\frac{7}{3}$.
如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则$\frac{AF}{EF}$=$\frac{7}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9-x2+2xy-y2=9-(-x2-2xy+y2) | B. | 9-x2+2xy-y2=9-(x2-2xy-y2) | ||
| C. | 9-x2+2xy-y2=9-(x2-2xy+y2) | D. | 9-x2+2xy-y2=9+(x2-2xy+y2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | 16.0 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 | 16.9 | 17.0 |
| x2 | 256 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 275.56 | 278.89 | 282.24 | 285.61 | 289 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
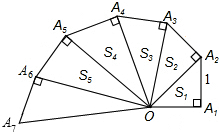 细心观察所示图形,认真分析各式,然后解答问题.
细心观察所示图形,认真分析各式,然后解答问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com