
【题目】攀枝花芒果由于品质高、口感好而闻名全国,通过优质快捷的网络销售渠道,小明的妈妈先购买了2箱A品种芒果和3箱B品种芒果,共花费450元;后又购买了l箱A品种芒果和2箱B品种芒果,共花费275元(每次两种芒果的售价都不变).
(1)问A品种芒果和B品种芒果的售价分别是每箱多少元?
(2)现要购买两种芒果共18箱,要求B品种芒果的数量不少于A品种芒果数量的2倍,但不超过A品种芒果数量的4倍,请你设计购买方案,并写出所需费用最低的购买方案.
【答案】(1)A品种芒果售价为每箱75元,B品种芒果售价为每箱100元;(2)购买方案有:A品种芒果4箱,B品种芒果14箱;A品种芒果5箱,B品种芒果13箱;A品种芒果6箱,B品种芒果12箱;其中购进A品种芒果6箱,B品种芒果12箱总费用最少.
【解析】试题分析:(1)设A品种芒果箱x元,B品种芒果为箱y元,根据题意列出方程组即可解决问题.
(2)设A品种芒果n箱,总费用为m元,则B品种芒果18﹣n箱,根据题意列不等式组即可得到结论.
试题解析:解:(1)设A品种芒果箱x元,B品种芒果为箱y元,根据题意得: ![]() ,解得:
,解得: ![]() .
.
答:A品种芒果售价为每箱75元,B品种芒果售价为每箱100元.
(2)设A品种芒果n箱,总费用为m元,则B品种芒果18﹣n箱,∴18﹣n≥2n且18﹣n≤4n,∴ ![]() ≤n≤6,∵n非负整数,∴n=4,5,6,相应的18﹣n=14,13,12;
≤n≤6,∵n非负整数,∴n=4,5,6,相应的18﹣n=14,13,12;
∴购买方案有:A品种芒果4箱,B品种芒果14箱;A品种芒果5箱,B品种芒果13箱;A品种芒果6箱,B品种芒果12箱;
∴所需费用m分别为:4×75+14×100=1700元;5×75+13×100=1675元;6×75+12×100=1650元,∴购进A品种芒果6箱,B品种芒果12箱总费用最少.


科目:初中数学 来源: 题型:
【题目】如图所示,OD,OE分别是∠AOC和∠BOC的平分线,∠AOD=40°,∠BOE=25°,求∠AOB的度数.
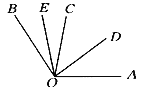
解:∵OD平分∠AOC,OE平分∠BOC(已知),
∴∠AOC=2∠AOD,∠BOC=2________( ),
∵∠AOD=40°,∠______=25°(已知),
∴∠AOC=2×40°=80°(等量代换),∠BOC=2×_____°=______°,
∴∠AOB=________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年“五一”假期期间,某市接待旅游总人数达到了9 180 000人次,将9 180 000用科学记数法表示应为( )
A.918×104
B.9.18×105
C.9.18×106
D.9.18×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(1)(-2)×(-2)2×(-2)3=_____________; (2)(-x)9·x5·(-x)5·(-x)3=___________;(3)an+4·a2n-1·a____________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫作点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,这样依次得到点A1,A2,A3,A4…,若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“十二五”期间,达州市经济保持稳步增长,地区生产总值约由819亿元增加到1351亿元,年均增长约10%,将1351亿元用科学记数法表示应为( )
A.1.351×1011
B.13.51×1012
C.1.351×1013
D.0.1351×1012
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将一个自然数各位上的数字按照从高位数字到低位数字排成一列后,后一个人数减去前一个数的差是一个常数,则这个数叫做“幸福数”.如:四位数2468排成一列后为:2,4,6,8.因为8-6=6-4=4-2=2,且差为2的常数,故2468是一个差为2的四位“幸福数”.又如,9876,6666等也是“幸福数”.
若一个自然数从左到右各数位上的数字和另一个自然数从右到左各数位上的数字完全相同,则称这两个数为“三生三世数”.例如:3579与9753,8765与5678,...,都是“三生三世数”.
规定:把高位数字为x,差为2的三位“幸福数”与它的“三生三世数”的和与222的商记为F(x).例如当x=5时,三位“幸福数”为579,它的“三生三世数”为975,三位“幸福数”与它的“三生三世数”的和为:579+975=1554,1554÷222=7,所以F(x)=7.
(1)计算:F(1), F(4);
(2)已知F(x) =4,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图6,已知箭头的方向是水流的方向,一艘游艇从江心岛的右侧A点逆流航行3小时到达B点后,又继续顺流航行2.5小时后到达C点,总共航行了208千米,已知水流的速度是2千米/时。
(1)求游艇在静水中的速度。
(2)由于AC段在建桥,游艇用同样的速度沿原路返回共需多少时间?(结果保留一位小数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副直角三角板按图11-14摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC,∠E=30°,∠BCE=40°.求∠CDF的度数.
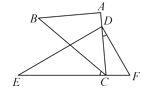
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com