
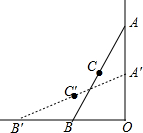
 如图,在直角∠O的内部有一滑动杆AB,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动,如果滑动杆从图中AB处滑动到A′B′处,那么滑动杆的中点C所经过的路径是( )
如图,在直角∠O的内部有一滑动杆AB,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动,如果滑动杆从图中AB处滑动到A′B′处,那么滑动杆的中点C所经过的路径是( )| A. | 直线的一部分 | B. | 圆的一部分 | C. | 双曲线的一部分 | D. | 抛物线的一部分 |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
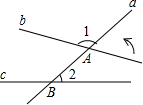 如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转15°.
如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转15°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某车间接到加工一批零件的任务,准备派甲、乙两名工人参与完成.乙比甲晚参加工作一段时间,工作期间甲工人因有事停工5天,若两人分得的工作量相等,各自的工作效率一定,他们各自的工作量y(个)随工作时间x(天)变化的图象如图所示,则有下列说法:
某车间接到加工一批零件的任务,准备派甲、乙两名工人参与完成.乙比甲晚参加工作一段时间,工作期间甲工人因有事停工5天,若两人分得的工作量相等,各自的工作效率一定,他们各自的工作量y(个)随工作时间x(天)变化的图象如图所示,则有下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≤2 | B. | 1≤a≤2 | C. | 1≤a<2 | D. | a≥1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
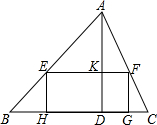 已知锐角△ABC中,边BC长为12,高AD长为8.
已知锐角△ABC中,边BC长为12,高AD长为8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,0) | B. | (0,2) | C. | (2,-4) | D. | (-4,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
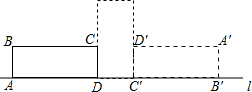 在矩形ABCD中,AB=5,AD=12,将矩形ABCD沿直线l向右翻滚两次至如图所示位置,则点B所经过的路线长是12.5π(结果不取近似值).
在矩形ABCD中,AB=5,AD=12,将矩形ABCD沿直线l向右翻滚两次至如图所示位置,则点B所经过的路线长是12.5π(结果不取近似值).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
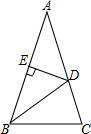 如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.
如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com