
科目:初中数学 来源: 题型:解答题
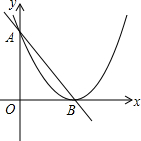 如图,直线y=-x+3交x轴于点B,交y轴于点A.抛物线的顶点为点B,且经过点A.
如图,直线y=-x+3交x轴于点B,交y轴于点A.抛物线的顶点为点B,且经过点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
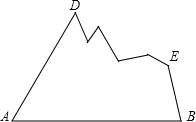 如图是举世闻名的三星堆考古中挖掘出的一个三角形残缺玉片,工作人员想制作该玉片模型,则测量图中哪些数据,就可制成符合规格的三角形玉片模型?请说明其中的道理.
如图是举世闻名的三星堆考古中挖掘出的一个三角形残缺玉片,工作人员想制作该玉片模型,则测量图中哪些数据,就可制成符合规格的三角形玉片模型?请说明其中的道理.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com