
【题目】如图,AB是⊙O的直径,过⊙O外一点P作⊙O的两条切线PC,PD,切点分别为C,D,连接OP,CD.
(1)求证:OP⊥CD;
(2)连接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)先判断出Rt△ODP≌Rt△OCP,得出∠DOP=∠COP,即可得出结论;
(2)先 求出∠COD=60°,得出△OCD是等边三角形,最后用锐角三角函数即可得出结论.
(1)证明:如图,连接OC,OD,则OC=OD.
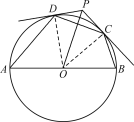
∵PD,PC是⊙O的切线,
∴∠ODP=∠OCP=90°.
在Rt△ODP和Rt△OCP中,
![]() ,
,
∴Rt△ODP≌Rt△OCP,
∴∠DOP=∠COP.
∵OD=OC,
∴OP⊥CD.
(2)连接AD,BC如图所示,则OA=OD=OC=OB=2,
∴∠ADO=∠DAO=50°,
∠BCO=∠CBO=70°,
∴∠AOD=80°,∠BOC=40°,
∴∠COD=60°.
∵OD=OC,
∴△COD是等边三角形.
由(1)知,∠DOP=∠COP=30°,
在Rt△ODP中,OP=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
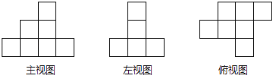
【题目】如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要________个小立方块.最终搭成的长方体的表面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为![]() (m2),种草所需费用
(m2),种草所需费用![]() 1(元)与
1(元)与![]() (m2)的函数关系式为
(m2)的函数关系式为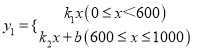 ,其图象如图所示:栽花所需费用
,其图象如图所示:栽花所需费用![]() 2(元)与x(m2)的函数关系式为
2(元)与x(m2)的函数关系式为![]() 2=﹣0.01
2=﹣0.01![]() 2﹣20
2﹣20![]() +30000(0≤
+30000(0≤![]() ≤1000).
≤1000).
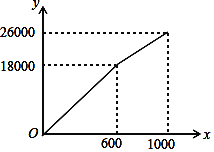
(1)请直接写出k1、k2和b的值;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与![]() 的函数关系式,求出绿化总费用W的最大值;
的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于700m2,栽花部分的面积不少于100m2,请求出绿化总费用W的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳市某校九年级有500名学生,在体育考试前随机抽取部分学生进行体能测试,成绩分别记为A、B、C、D共四个等级,其中A级和B级成绩为“优”,将测试结果绘制成如下条形统计图和扇形统计图.
成绩频数条形统计图 成绩频数扇形统计图
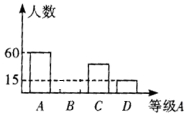
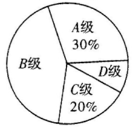
(1)求抽取参加体能测试的学生人数;
(2)补全条形统计图;
(3)估计该校九年级全体学生参加体能测试成绩为“优”的学生共有多少人?(精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
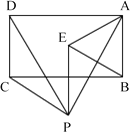
【题目】如图,P是矩形ABCD下方一点,将△PCD绕点P顺时针旋转60°后,恰好点D与点A重合,得到△PEA,连接EB,问:△ABE是什么特殊三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
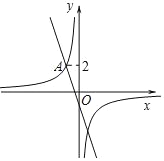
【题目】如图,在平面直角坐标系xOy中,直线y=kx+m与双曲线y=﹣![]() 相交于点A(m,2).
相交于点A(m,2).
(1)求直线y=kx+m的表达式;
(2)直线y=kx+m与双曲线y=﹣![]() 的另一个交点为B,点P为x轴上一点,若AB=BP,直接写出P点坐标.
的另一个交点为B,点P为x轴上一点,若AB=BP,直接写出P点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com