
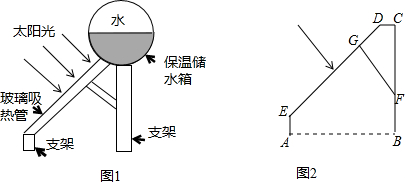
分析 (1)作EP⊥BC、DQ⊥EP,知CD=PQ=10,∠2+∠3=90°,由∠1+∠θ=90°且∠1=∠2知∠3=∠θ=37°50′,根据EQ=DEsin∠3和AB=EP=EQ+PQ可得答案;
(2)延长ED、BC交于点K,结合(1)知∠θ=∠3=∠K=60°,从而由CK=$\frac{CD}{tan∠K}$、KF=$\frac{GF}{sin∠K}$可得答案.
解答 解:(1)如图,作EP⊥BC于点P,作DQ⊥EP于点Q,
则CD=PQ=10,∠2+∠3=90°,
∵∠1+∠θ=90°,且∠1=∠2,
∴∠3=∠θ=37°50′,
则EQ=DEsin∠3=120×sin37°50′,
∴AB=EP=EQ+PQ=120sin37°50′+10=83.2,
故答案为:83.2;
(2)如图,延长ED、BC交于点K,
由(1)知∠θ=∠3=∠K=60°,
在Rt△CDK中,CK=$\frac{CD}{tan∠K}$=$\frac{10}{\sqrt{3}}$,
在Rt△KGF中,KF=$\frac{GF}{sin∠K}$=$\frac{30}{\frac{\sqrt{3}}{2}}$=$\frac{60}{\sqrt{3}}$,
则CF=KF-KC=$\frac{60}{\sqrt{3}}$-$\frac{10}{\sqrt{3}}$=$\frac{50}{\sqrt{3}}$=$\frac{50\sqrt{3}}{3}$.
点评 本题主要考查解直角三角形的应用,根据题意构建所需直角三角形和熟练掌握三角函数是解题的关键.


科目:初中数学 来源: 题型:解答题
| 运行区间 | 公布票价 | 学生票价 | ||
| 上车站 | 下车站 | 一等座 | 二等座 | 三等座 |
| 无锡 | 上海 | 81(元) | 68(元) | 51(元) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{1}{2}$ | B. | $\frac{13}{2}$ | C. | $\frac{17}{2}$ | D. | $\frac{25}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥1 | B. | x≥2 | C. | x>1 | D. | x>2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
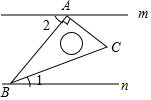 已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为( )
已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为( )| A. | 20° | B. | 30° | C. | 45° | D. | 50° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com