
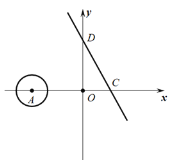
【题目】如图,在平面直角坐标系中,直线l的表达式是![]() ,它与两坐标轴分别交于C、D两点,且∠OCD=60,设点A的坐标为(m,0),若以A为圆心,2为半径的⊙A与直线l相交于M、N两点,当MN=
,它与两坐标轴分别交于C、D两点,且∠OCD=60,设点A的坐标为(m,0),若以A为圆心,2为半径的⊙A与直线l相交于M、N两点,当MN=![]() 时,m的值为( )
时,m的值为( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,抛物线![]() 经过点A(-2,0),B(4,0)两点,与
经过点A(-2,0),B(4,0)两点,与![]() 轴交于点C,点D是抛物线上一个动点,设点D的横坐标为
轴交于点C,点D是抛物线上一个动点,设点D的横坐标为![]() .连接AC,BC,DB,DC,
.连接AC,BC,DB,DC,
(1)求抛物线的函数表达式;
(2)△BCD的面积等于△AOC的面积的![]() 时,求
时,求![]() 的值;
的值;
(3)在(2)的条件下,若点M是![]() 轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙、丁从笔试、面试两个方面进行量化考核.甲、乙、丙、丁两项得分如下表:(单位:分)
甲 | 乙 | 丙 | 丁 | |
笔试 |
|
|
|
|
面试 |
|
|
|
|
(1)这![]() 名选手笔试成绩的中位数是____________分,面试的众数是_____________分;
名选手笔试成绩的中位数是____________分,面试的众数是_____________分;
(2)该公司规定:笔试、面试分别按![]() ,
,![]() 的比例计总分,请比较甲、乙的总分的大小.
的比例计总分,请比较甲、乙的总分的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,反比例函数和二次函数y=a(x2+x﹣1)的图象交于点A(1,a)和点B(﹣1,﹣a).
(1)求直线AB与y轴的交点坐标;
(2)要使上述反比例函数和二次函数在某一区域都是y随着x的增大而增大,求a应满足的条件以及x的取值范围;
(3)设二次函数的图象的顶点为Q,当Q在以AB为直径的圆上时,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
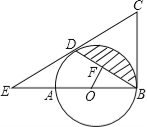
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在木里县某林场东西方向的两地之间修一条公路MN,已知点C周围200 m范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600 m到达B处,测得C在点B的北偏西60°方向上.
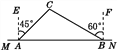
(1)MN是否穿过原始森林保护区?为什么?(参考数据: ![]() ≈1.732)
≈1.732)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市雷雷服饰有限公司生产了一款夏季服装,通过实验商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量![]() (百件)与时间
(百件)与时间![]() (
(![]() 为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量
为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量![]() (百件)与时间
(百件)与时间![]() (
(![]() 为整数,单位:天)的关系如下图所示.
为整数,单位:天)的关系如下图所示.
时间 | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
日销售量 | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
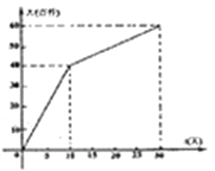
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映![]() 与
与![]() 的变化规律,并求出
的变化规律,并求出![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(2)求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为![]() (百件),求
(百件),求![]() 与
与![]() 的函数关系式;当
的函数关系式;当![]() 为何值时,日销售总量
为何值时,日销售总量![]() 达到最大,并求出此时的最大值.
达到最大,并求出此时的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并按要求完成相应的任务.
已知平面上两点![]() ,则所有符合
,则所有符合![]() 且
且![]() 的点
的点![]() 会组成一个圆.这个结论最先由古希腊数学家阿波罗尼斯发现,称阿氏圆.
会组成一个圆.这个结论最先由古希腊数学家阿波罗尼斯发现,称阿氏圆.
阿氏圆基本解法:构造三角形相似.
(问题)如图1,在平面直角坐标中,在![]() 轴,
轴,![]() 轴上分别有点
轴上分别有点![]() ,点
,点![]() 是平面内一动点,且
是平面内一动点,且![]() ,设
,设![]() ,求
,求![]() 的最小值.
的最小值.

阿氏圆的关键解题步骤:
第一步:如图1,在![]() 上取点
上取点![]() ,使得
,使得![]() ;
;
第二步:证明![]() ;第三步:连接
;第三步:连接![]() ,此时
,此时![]() 即为所求的最小值.
即为所求的最小值.
下面是该题的解答过程(部分):
解:在![]() 上取点
上取点![]() ,使得
,使得![]() ,
,
又![]() .
.
任务:
![]() 将以上解答过程补充完整.
将以上解答过程补充完整.
![]() 如图2,在
如图2,在![]() 中,
中,![]() 为
为![]() 内一动点,满足
内一动点,满足![]() ,利用
,利用![]() 中的结论,请直接写出
中的结论,请直接写出![]() 的最小值.
的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com