
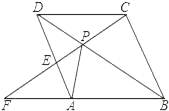
【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.
(1)图中△APD与哪个三角形全等:_____.
(2)猜想:线段PC、PE、PF之间存在什么关系:_____.
【答案】(1)△APD≌△CPD(SAS);(2) PC2=PEPF.
【解析】
(1)根据菱形的性质得∠ADP=∠CDP,DA=DC,从而得到△APD与△CPD全等.
(2)根据菱形的对边互相平行得∠DCF=∠F,再根据(1)题的结论得到∠DCP=∠DAP,从而证得△PAE∽△PFA,然后利用比例线段证得等积式即可.
(1)∵四边形ABCD为菱形,
∴∠ADP=∠CDP,DC=DA,
在△APD和△CPD中,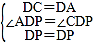 ,
,
∴△APD≌△CPD(SAS);
(2)∵四边形ABCD为菱形,
∴∠DCF=∠F,
∵△APD≌△CPD,
∴∠DCP=∠DAP,
∴∠F=∠PAE,
∠APE=∠FPA
∴△PAE∽△PFA,
∴![]() ,
,
即:PA2=PEPF,
∵P是菱形ABCD的对角线BD上一点,
∴PA=PC,
∴PC2=PEPF.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论;
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,猜测MN与BM的数量关系,无需证明.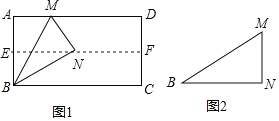
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
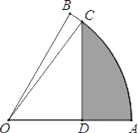
【题目】如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在![]() 上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为_____.
上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点![]() 出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到
出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到![]() (0,1),
(0,1),![]() (1,1),
(1,1),![]() (1,0),
(1,0),![]() (2,0),…那么点
(2,0),…那么点![]() 的坐标为__________.
的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
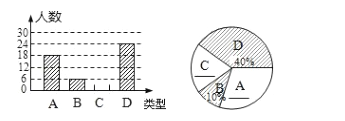
【题目】学校调查了某班同学上学的方式有四种:骑自行车、步行、乘坐公交车和家长接送(分别用A、B、C、D表示),根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请集合图中所给信息解答下列问题:
(1)这个班级学生共有多少人?
(2)将两幅不完整的图补充完整;
(3)求扇形统计图中C所对圆心角的度数;
(4)已知步行上学的同学中有3名女同学,学校将从步行上学的同学中随机选出2名同学参加交通安全知识培训,求所选2名同学恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,图形G上点P(x,y)的纵坐标y与其横坐标x的差y﹣x称为P点的“坐标差”,记作Zp,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”.
(1)①点A(3,1)的“坐标差”为_______;
②抛物线y=﹣x2+5x的“特征值”为________;
(2)某二次函数y=﹣x2+bx+c(c≠0)的“特征值”为﹣1,点B(m,0)与点C分别是此二次函数的图象与x轴和y轴的交点,且点B与点C的“坐标差”相等.
①直接写出m=______;(用含c的式子表示)
②求此二次函数的表达式.
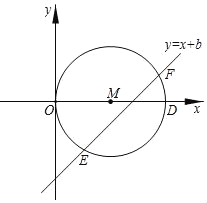
(3)如图,在平面直角坐标系xOy中,点D(4,0),以OD为直径作⊙M,直线y=x+b与⊙M相交于点E、F.
①比较点E、F的“坐标差”ZE、ZF的大小.
②请直接写出⊙M的“特征值”为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com