
如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.
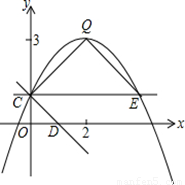
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;
(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
解:(1)∵C(0,1),OD=OC,∴D点坐标为(1,0)。
设直线CD的解析式为y=kx+b(k≠0),
将C(0,1),D(1,0)代入得: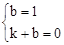 ,解得:。
,解得:。
∴直线CD的解析式为:y=﹣x+1。
(2)设抛物线的解析式为y=a(x﹣2)2+3,
将C(0,1)代入得:1=a×(﹣2)2+3,解得a=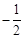 。
。
∴y=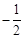 (x﹣2)2+3=
(x﹣2)2+3=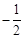 x2+2x+1。
x2+2x+1。
(3)证明:由题意可知,∠ECD=45°,
∵OC=OD,且OC⊥OD,∴△OCD为等腰直角三角形,∠ODC=45°。
∴∠ECD=∠ODC,∴CE∥x轴。
∴点C、E关于对称轴(直线x=2)对称,
∴点E的坐标为(4,1)。
如答图①所示,设对称轴(直线x=2)与CE交于点F,
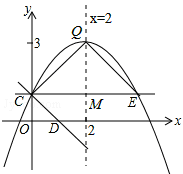
则F(2,1)。
∴ME=CM=QM=2。
∴△QME与△QMC均为等腰直角三角形。
∴∠QEC=∠QCE=45°。
又∵△OCD为等腰直角三角形,
∴∠ODC=∠OCD=45°。
∴∠QEC=∠QCE=∠ODC=∠OCD=45°。∴△CEQ∽△CDO。
(4)存在。
如答图②所示,作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度。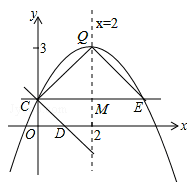
(证明如下:不妨在线段OD上取异于点F的任一点F′,在线段QE上取异于点P的任一点P′,连接F′C″,F′P′,P′C′.
由轴对称的性质可知,△P′CF′的周长=F′C″+F′P′+P′C′。
而F′C″+F′P′+P′C′是点C′,C″之间的折线段,
由两点之间线段最短可知:F′C″+F′P′+P′C′>C′C″,即△P′CF′的周长大于△PCE的周长。)
如答图③所示,连接C′E,
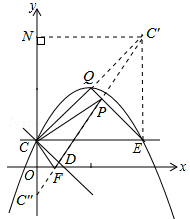
∵C,C′关于直线QE对称,△QCE为等腰直角三角形,
∴△QC′E为等腰直角三角形。
∴△CEC′为等腰直角三角形。
∴点C′的坐标为(4,5)。
∵C,C″关于x轴对称,∴点C″的坐标为(﹣1,0)。
过点C′作C′N⊥y轴于点N,则NC′=4,NC″=4+1+1=6,
在Rt△C′NC″中,由勾股定理得:
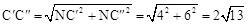 。
。
综上所述,在P点和F点移动过程中,△PCF的周长存在最小值,最小值为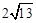 。
。
【解析】(1)利用待定系数法求出直线解析式。
(2)利用待定系数法求出抛物线的解析式。
(3)关键是证明△CEQ与△CDO均为等腰直角三角形。
(4)如答图②所示,作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度。
利用轴对称的性质、两点之间线段最短可以证明此时△PCF的周长最小。
如答图③所示,利用勾股定理求出线段C′C″的长度,即△PCF周长的最小值。


科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 9 |
| 8 |
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少?查看答案和解析>>
科目:初中数学 来源: 题型:
 O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1.查看答案和解析>>
科目:初中数学 来源: 题型:
 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12,查看答案和解析>>
科目:初中数学 来源: 题型:
 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com