
【题目】如图,正方形![]() 的边
的边![]() 、
、![]() 在坐标轴上,点
在坐标轴上,点![]() 坐标为
坐标为![]() ,将正方形
,将正方形![]() 绕点
绕点![]() 逆时针旋转角度
逆时针旋转角度![]()
![]() ,得到正方形
,得到正方形![]() ,
, ![]() 交线段
交线段![]() 于点
于点![]() ,
, ![]() 的延长线交线段
的延长线交线段![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() .
.

(1)求证:![]() 平分
平分 ![]() ;
;
(2)在正方形![]() 绕点
绕点![]() 逆时针旋转的过程中,求线段
逆时针旋转的过程中,求线段![]() 、
、![]() 、
、![]() 之间的数量关系;
之间的数量关系;
(3)连结![]() 、
、![]() 、
、![]() 、
、![]() ,在旋转的过程中,四边形
,在旋转的过程中,四边形![]() 是否能在点G满足一定的条件下成为矩形?若能,试求出直线
是否能在点G满足一定的条件下成为矩形?若能,试求出直线![]() 的解析式;若不能,请说明理由.
的解析式;若不能,请说明理由.
【答案】(1)证明见解析(2)证明见解析(3)![]() .
.
【解析】试题分析:(1)根据旋转和正方形的性质可以得出CD=CB,∠CDG=∠CBG=90°,根据全等三角形的判定定理(HL)即可证出Rt△CDG≌Rt△CBG,即∠ DCG=∠BCG,由此即可得出CG平分∠DCB;
(2)由(1)的Rt△CDG≌Rt△CBG,可得出BG=DG,根据直角三角形的判定定理(HL)即可证出Rt△CHO≌Rt△CHD,即OH=HD,再根据线段间的关系即可得出![]() ;
;
(3)根据(2)的结论即可找出当G点为AB的中点时,四边形AEBD为矩形,再根据正方形的性质以及点B的坐标可得出点G的坐标,设H点的坐标为![]() ,由此可得出
,由此可得出![]() ,根据勾股定理即可求得
,根据勾股定理即可求得![]() 的值,即可得出点H的坐标,结合点H、G的坐标利用待定系数法即可求得直线DE的解析式.
的值,即可得出点H的坐标,结合点H、G的坐标利用待定系数法即可求得直线DE的解析式.
试题解析:(1)证明:
∵正方形![]() 绕点
绕点![]() 旋转得到正方形
旋转得到正方形![]() ,
,
∴![]() ,
, ![]() ,
,
在![]() 和
和![]() 中,
中, ![]() ,
,
∴![]() ≌
≌![]()
![]() ,
,
∴![]() ,
,
即![]() 平分
平分![]() .
.

(2)由(1)证得: ![]() ≌
≌![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中, ![]() ,
,
∴![]() ≌
≌![]()
![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)四边形![]() 可为矩形..
可为矩形..
当![]() 点为
点为![]() 中点时,四边形
中点时,四边形![]() 为矩形.如图,
为矩形.如图, ![]() ,
,
由(2)证得: ![]() ,又
,又![]() ,
,
则![]() ,
,
∴四边形![]() 为矩形..
为矩形..
∵点B坐标为(6,6),
∴ AB=6,∴![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() ..
..
设![]() 点的坐标为
点的坐标为![]() ,则
,则![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,由勾股定理得:
,由勾股定理得: ![]() ,
,
解得: ![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() .
.
设直线![]() 的解析式为:
的解析式为: ![]()
![]() ,
,
又直线![]() 过点
过点![]()
![]() 、
、![]() ,∴
,∴![]() ,解得:
,解得:  ,
,
∴ 直线![]() 的解析式为:
的解析式为: ![]() .
.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,∠ABC的两边分别平行于∠DEF的两边,且∠ABC=25°.
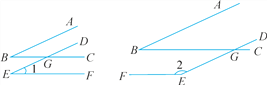
(1)∠1= ,∠2= .
(2)请观察∠1,∠2与∠ABC分别有怎样的关系,请你由此归纳一个真命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校操场的环形跑道长400米,小聪的爸爸陪小聪锻炼,小聪跑步每秒行2.5米,爸爸骑自行车每秒行5.5米,两人从同一地点出发,反向而行,每隔_____秒两人相遇一次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋数学家杨辉曾提出这样一个问题:“直田积(矩形面积),八百六十四(平方步),只云阔(宽)不及长一十二步(宽比长少12步),问阔及长各几步.”如果设矩形田地的长为x步,那么根据题意列出的方程为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
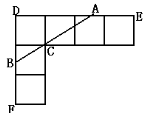
【题目】已知:正方形的边长为1.(1)如图(a),可以计算出正方形的对角线长为![]() .如图(b),求两个并排成的矩形的对角线的长.n个呢?(2)若把(c)(d)两图拼成如下“L”形,过C作直线交DE于A,交DF于B.若DB=
.如图(b),求两个并排成的矩形的对角线的长.n个呢?(2)若把(c)(d)两图拼成如下“L”形,过C作直线交DE于A,交DF于B.若DB=![]() ,求DA的长度.
,求DA的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是以PQ为底的等腰三角形时,运动的时间是( )

A.2.5秒 B.3秒 C.3.5秒 D.4秒
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com