

���� ��1���������ߣ�����ƽ�����ƣ��á�BDE�ס�OAE���������������ζ�Ӧ�ߵıȵ������Ʊ���ʽ���EH�ij�������E�������ꣻ�ٸ��ݹ��ɶ�����30�����OH������E�ĺ����꣬��E��3$\sqrt{3}$��3����
��2���ȼ����P��x����ʱt=2��ֱ�߹���Eʱ��t=3��
������������ۣ��ٵ�0��t��2ʱ����ͼ3����MNP���OAB�ص����ֵ����Ϊ���ε������
�ڵ�2��t��3ʱ����ͼ4����MNP���OAB�ص����ֵ����Ϊ��PMN�������
�۵�3��t��4ʱ����ͼ5����MNP���OAB�ص����ֵ����Ϊ��PMN�������һ�룻
��3�����ڣ���ΪS��ABD=$\frac{8\sqrt{3}}{3}$�����ݣ�2�������S��ֵ���뵽S=$\frac{1}{2}$S��ABD�ֱ��з��̣�������ɣ�
��� �⣨1����ͼ1����E��GH��OA����BC��G����OA��H����GH��BC��
���ı���OABC�Ǿ��Σ�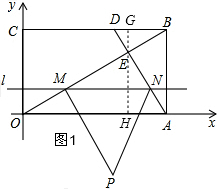
��BC��OA��BC=OA��
��B��4$\sqrt{3}$��4����
��OA=4$\sqrt{3}$��AB=GH=4��
�ɹ��ɶ����ã�OB=$\sqrt{{4}^{2}+��4\sqrt{3}��^{2}}$=8��
���EOA=30�㣬
��BC��OA��
���BDE�ס�OAE��
��$\frac{BD}{OA}=\frac{EG}{EH}$��
��CD��DB=2��1��
��$\frac{BD}{OA}=\frac{EG}{EH}$=$\frac{1}{3}$��
��EH=3��
��OE=2EH=6��
��OH=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$��
��E��3$\sqrt{3}$��3����
��2����ͼ1���ھ���OABC�У�
�ߵ�B������Ϊ��4$\sqrt{3}$��4������CD��DB=2��1��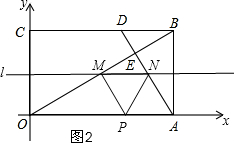
��A��4$\sqrt{3}$��0����D��$\frac{8\sqrt{3}}{3}$��4����
�ɵ�ֱ��OB�Ľ���ʽΪ��y1=$\frac{\sqrt{3}}{3}$x��
ֱ��AD�Ľ���ʽΪ��y2=-$\sqrt{3}$x+12��
��y1=y2=tʱ���ɵõ�M��N�ĺ�����ֱ�Ϊ��
xM=$\sqrt{3}$t��xN=4$\sqrt{3}$-$\frac{\sqrt{3}}{3}$t��
��MN=|xM-xN|=|4$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$t|��
����P�˶���x��ʱ����ͼ2��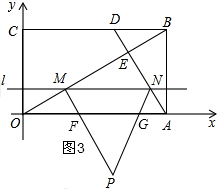
�ߡ�MNP�ǵȱ������Σ�
��MN•sin60��=t�����t=2��
��t=3ʱ��M��N��P�����غϣ�S=0��
���ۣ��ٵ�0��t��2ʱ����ͼ3����PM��PN�ֱ�x���ڵ�F��G��
���PFG�ĸ�ΪMN•sin60��-t=6-3t��
���PFG�ı߳�Ϊ$\frac{6-3t}{sin60��}$=4$\sqrt{3}$-2$\sqrt{3}$t��
��MN=xN-xM=4$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$t��
��S=S����FGNM��
=$\frac{1}{2}$t��4$\sqrt{3}$-2$\sqrt{3}$t+4$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$t����
=-$\frac{5\sqrt{3}}{3}$t2+4$\sqrt{3}$t��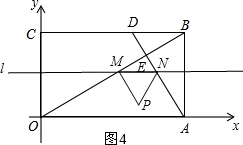
�ڵ�2��t��3ʱ����ͼ4��
��ʱ�ȱߡ�MNP�������ڡ�OAB�ڣ�
���PMN�ĸ�ΪMN•sin60��=6-2t��
��MN=xN-xM=4$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$t��
��S=S��MNP
=$\frac{1}{2}$��6-2t����4$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$t��
=$\frac{4\sqrt{3}}{3}{t}^{2}$-8$\sqrt{3}$t+12$\sqrt{3}$��
�۵�3��t��4ʱ����ͼ5��
��Rt��OAB�У���AOB=30�㣬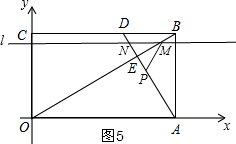
���NME=30�㣬
��ȱߡ�NMP����ֱ��OB�Գƣ�
��MN=|xN-xM|=$\frac{4\sqrt{3}}{3}$t-4$\sqrt{3}$��
��S=$\frac{1}{2}$S��MNP
=$\frac{1}{2}$��$\frac{1}{2}$��2t-6����-4$\sqrt{3}$+$\frac{4\sqrt{3}}{3}$t��
=$\frac{2\sqrt{3}}{3}{t}^{2}$-4$\sqrt{3}$t+6$\sqrt{3}$��
�����������ٵ�0��t��2ʱ��S=-$\frac{5\sqrt{3}}{3}$t2+4$\sqrt{3}$t��
�ڵ�2��t��3ʱ��S=$\frac{4\sqrt{3}}{3}{t}^{2}$-8$\sqrt{3}$t+12$\sqrt{3}$��
�۵�3��t��4ʱ��S=$\frac{2\sqrt{3}}{3}{t}^{2}$-4$\sqrt{3}$t+6$\sqrt{3}$��
�ܵ�t=3ʱ��S=0��
��3������t��ֵ��ʹS=$\frac{1}{2}$S��ABD������
��S��ABD=$\frac{8\sqrt{3}}{3}$����S=$\frac{1}{2}$S��ABD��������
�ٵ�0��t��2ʱ����-$\frac{5\sqrt{3}}{3}{t}^{2}$+4$\sqrt{3}$t=$\frac{4\sqrt{3}}{3}$��
��ã�t1=2����ȥ����t2=$\frac{2}{5}$��
�ڵ�2��t��3ʱ����$\frac{4\sqrt{3}}{3}{t}^{2}$-8$\sqrt{3}$t+12$\sqrt{3}$=$\frac{4\sqrt{3}}{3}$��
��ã�t1=2��t2=4����ȥ����
�۵�3��t��4ʱ����$\frac{2\sqrt{3}}{3}{t}^{2}$-4$\sqrt{3}$t+6$\sqrt{3}$=$\frac{4\sqrt{3}}{3}$��
t1=3+$\sqrt{2}$��4���ᣩ��t2=3-$\sqrt{2}$��3���ᣩ��
�����������t��2��$\frac{2}{5}$��
���� �������ı��ε��ۺ��⣬�����˾��Ρ��ȱ������Ρ���ֱ�������Ρ����������ε�ͼ�ε����ʣ��������Ƚϴ�ͬʱҲ���˶������⣬��ֱ���˶��ɵ�ͼ������������˷������۵�˼�룬�ۺ��Խ�ǿ������ؼ���������ֱ�ߵ��ж��켣����ȷ�ȱߡ�MNP�Ĵ�С��λ�ã�


 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij����Ϊ�˲ⶨij��ʱ�������̨���ŷ�����ͳ�������ʱ��α����й˿�������̨�ŶӸ���ĵȴ�ʱ�䣬�����Ƴ����µ�Ƶ���ֲ�ֱ��ͼ��ͼ�еȴ�ʱ��2���ӵ�3���ӱ�ʾ���ڻ����2���Ӷ�С��3���ӣ�������ͬ�������ʱ����ڹ˿͵ȴ�ʱ�䲻����6���ӵ�����Ϊ7��
ij����Ϊ�˲ⶨij��ʱ�������̨���ŷ�����ͳ�������ʱ��α����й˿�������̨�ŶӸ���ĵȴ�ʱ�䣬�����Ƴ����µ�Ƶ���ֲ�ֱ��ͼ��ͼ�еȴ�ʱ��2���ӵ�3���ӱ�ʾ���ڻ����2���Ӷ�С��3���ӣ�������ͬ�������ʱ����ڹ˿͵ȴ�ʱ�䲻����6���ӵ�����Ϊ7���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | ���� | C�� | ���� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ijѧУΪ���˽�ѧ���Ŀ����Ķ���������������50��ѧ�����õ�������ijһ����Կ����Ķ����õ�ʱ������ݣ������ͼ��ʾ�����ݴ�����ͳ��ͼ������һ���Уѧ��ƽ�������Ķ�ʱ��ԼΪ��������
ijѧУΪ���˽�ѧ���Ŀ����Ķ���������������50��ѧ�����õ�������ijһ����Կ����Ķ����õ�ʱ������ݣ������ͼ��ʾ�����ݴ�����ͳ��ͼ������һ���Уѧ��ƽ�������Ķ�ʱ��ԼΪ��������| A�� | 0.96ʱ | B�� | 1.07ʱ | C�� | 1.15ʱ | D�� | 1.50ʱ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
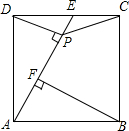 ��ͼ��������ABCD�У���EΪCD���е㣬DP��AE������ΪP�㣬BF��AE��F��
��ͼ��������ABCD�У���EΪCD���е㣬DP��AE������ΪP�㣬BF��AE��F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD�������Խ����ཻ�ڵ�O����DAC=30�㣬BD=12
��ͼ������ABCD�������Խ����ཻ�ڵ�O����DAC=30�㣬BD=12�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com