
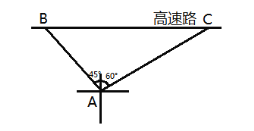
”¾ĢāÄæ”æŗܶą½»ĶØŹĀ¹ŹŹĒÓÉÓŚ³¬ĖŁŠŠŹ»µ¼ÖĀµÄ£¬ĪŖ¼ÆÖŠÖĪĄķ³¬ĖŁĻÖĻó£¬øßĖŁ½»¾ÆŌŚ¾ąĄėøßĖŁĀ·40Ć׵ĵŲ·½ÉčÖĆĮĖŅ»øö²āĖŁ¹Ū²ģµć£¬ĻÖ²āµĆ²āĖŁµćµÄĪ÷±±·½ĻņÓŠŅ»Į¾Š”ŠĶ½Ī³µ“ÓB“¦ŃŲĪ÷ĻņÕż¶«·½ĻņŠŠŹ»£¬2ĆėÖÓŗ󵽓ļ²āĖŁµć±±Ę«¶«![]() µÄ·½ĻņÉĻµÄC“¦£¬ČēĶ¼£®
µÄ·½ĻņÉĻµÄC“¦£¬ČēĶ¼£®
£Ø1£©ĒóøĆŠ”ŠĶ½Ī³µŌŚ²āĖŁ¹ż³ĢÖŠµÄĘ½¾łŠŠŹ»ĖŁ¶ČŌ¼ŹĒ¶ąÉŁĒ§Ć×/Ź±£Ø¾«Č·µ½1Ē§Ć×/Ź±£©£æ
£Ø²Īæ¼Źż¾Ż£ŗ![]() £©
£©
£Ø2£©ĪŅ¹ś½»Ķطعę¶Ø£ŗŠ”½Ī³µŌŚøßĖŁĀ·ŠŠŹ»£¬Ź±ĖŁ³¬¹żĻŽ¶ØĖŁ¶Č10%ŅŌÉĻ²»µ½50%µÄ“¦200ŌŖ·£æī£¬æŪ3·Ö£»Ź±ĖŁ³¬¹żĻŽ¶ØĖŁ¶Č50%ŅŌÉĻ²»µ½70%µÄ“¦1500ŌŖ·£æī£¬æŪ12·Ö£»Ź±ĖŁ³¬¹żĻŽ¶ØŹ±ĖŁ70%ŅŌÉĻµÄ“¦1500ŌŖ·£æī£¬æŪ12·Ö£®ČōøĆøßĖŁĀ·¶ĪĻŽĖŁ120Ē§Ć×/Ź±£¬ÄćČĻĪŖøĆŠ”½Ī³µ¼ŻŹ»Ō±»įŹÜµ½ŌõŃłµÄ“¦·££®
”¾“š°ø”æ£Ø1£©197Ē§Ć×/Ź±£»£Ø2£©Š”½Ī³µµÄ¼ŻŹ»Ō±»įŹÜµ½1500ŌŖ·£æī£¬æŪ12·ÖµÄ“¦·££®
”¾½āĪö”æ
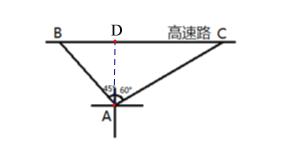
£Ø1£©¹żµćA×÷AD”ĶBCÓŚµćD£¬ŌņAD=40m£¬Ķعż½āÖ±½ĒČż½ĒŠĪ£¬Ēó³öBD£¬CDµÄ³¤£¬“Ó¶ųĒó³öBCµÄ³¤£¬½ų¶ų¼“æÉĒó³öĖŁ¶Č£»
£Ø2£©Ēó³öŠ”½Ī³µµÄ³¬ĖŁ·¶Ī§£¬¼“æɵƵ½½įĀŪ£®
£Ø1£©¹żµćA×÷AD”ĶBCÓŚµćD£¬ŌņAD=40m£¬
”ß”ĻBAD=45”ć£¬
”ą”ĻABD=45”ć£¬
”ąBD=AD=40m£¬
”ß”ĻDAC=60”ć£¬
”ąCD=AD”Įtan60”ć=40![]() m£¬
m£¬
”ąBC=40+40![]() ”Ö109.28m£¬
”Ö109.28m£¬
”ąŠ”½Ī³µµÄĖŁ¶Č=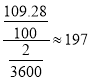 £ØĒ§Ć×/Š”Ź±£©£¬
£ØĒ§Ć×/Š”Ź±£©£¬
“š£ŗøĆŠ”ŠĶ½Ī³µŌŚ²āĖŁ¹ż³ĢÖŠµÄĘ½¾łŠŠŹ»ĖŁ¶ČŌ¼ŹĒ197Ē§Ć×/Ź±£»
£Ø2£©£Ø197-120£©”Ā120”Ö0.64=64£„£¬
”ß50£„£¼64£„£¼70£„£¬
”ąŠ”½Ī³µµÄ¼ŻŹ»Ō±»įŹÜµ½1500ŌŖ·£æī£¬æŪ12·ÖµÄ“¦·££®


 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCµÄ¶„µć×ų±ź·Ö±šĪŖA£Ø©6£¬0£©£¬B£Ø4£¬0£©£¬C£Ø0£¬8£©£¬°Ń”÷ABCŃŲÖ±ĻßBC·ÕŪ£¬µćAµÄ¶ŌÓ¦µćĪŖD£¬Å×ĪļĻßy=ax2©10ax+c¾¹żµćC£¬¶„µćMŌŚÖ±ĻßBCÉĻ£®

£Ø1£©Ö¤Ć÷ĖıߊĪABCDŹĒĮāŠĪ£¬²¢ĒóµćDµÄ×ų±ź£»
£Ø2£©ĒóÅ×ĪļĻߵĶŌ³ĘÖįŗĶŗÆŹż±ķ“ļŹ½£»
£Ø3£©ŌŚÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹µĆ”÷PBDÓė”÷PCDµÄĆ껿ĻąµČ£æČō“ęŌŚ£¬Ö±½ÓŠ“³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
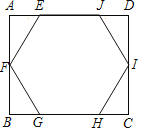
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠÓŠŅ»øöÕżĮł±ßŠĪEFGHIJ£¬Ę䶄µć¾łŌŚ¾ŲŠĪµÄ±ßÉĻ£¬±ßEJŗĶ±ßGH·Ö±šŌŚ¾ŲŠĪµÄ±ßADŗĶBCÉĻ£¬Ōņ![]() £½_____£®
£½_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
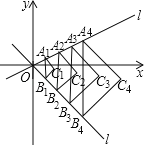
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬”÷A1B1C1£¬”÷A2B2C2£¬”÷A3B3C3£¬”£¬”÷AnBnCn¾łĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬ĒŅ”ĻC1£½”ĻC2£½”ĻC3£½”£½”ĻCn£½90”ć£¬µćA1£¬A2£¬A3£¬”£¬AnŗĶµćB1£¬B2£¬B3£¬”£¬Bn·Ö±šŌŚÕż±ČĄżŗÆŹży£½![]() xŗĶy£½©xµÄĶ¼ĻóÉĻ£¬ĒŅµćA1£¬A2£¬A3£¬”£¬AnµÄŗį×ų±ź·Ö±šĪŖ1£¬2£¬3”n£¬Ļ߶ĪA1B1£¬A2B2£¬A3B3£¬”£¬AnBn¾łÓėyÖįĘ½ŠŠ£®°“ÕÕĶ¼ÖŠĖł·“Ó³µÄ¹ęĀÉ£¬Ōņ”÷AnBnCnµÄ¶„µćCnµÄ×ų±źŹĒ____£®£ØĘäÖŠnĪŖÕżÕūŹż£©
xŗĶy£½©xµÄĶ¼ĻóÉĻ£¬ĒŅµćA1£¬A2£¬A3£¬”£¬AnµÄŗį×ų±ź·Ö±šĪŖ1£¬2£¬3”n£¬Ļ߶ĪA1B1£¬A2B2£¬A3B3£¬”£¬AnBn¾łÓėyÖįĘ½ŠŠ£®°“ÕÕĶ¼ÖŠĖł·“Ó³µÄ¹ęĀÉ£¬Ōņ”÷AnBnCnµÄ¶„µćCnµÄ×ų±źŹĒ____£®£ØĘäÖŠnĪŖÕżÕūŹż£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻß![]() ½»yÖįÓŚµćB£Ø0£¬3£©£¬½»xÖįÓŚA£¬CĮ½µć£¬Cµć×ų±ź£Ø4£¬0£©£¬µćPŹĒBCÉĻ·½Å×ĪļĻßÉĻŅ»¶Æµć(P²»ÓėB£¬CÖŲŗĻ)£®
½»yÖįÓŚµćB£Ø0£¬3£©£¬½»xÖįÓŚA£¬CĮ½µć£¬Cµć×ų±ź£Ø4£¬0£©£¬µćPŹĒBCÉĻ·½Å×ĪļĻßÉĻŅ»¶Æµć(P²»ÓėB£¬CÖŲŗĻ)£®
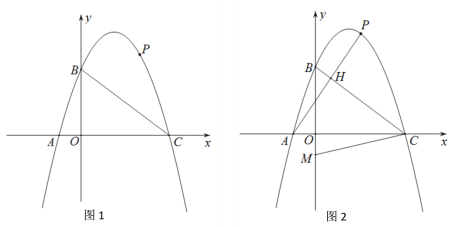
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ČōµćPµ½Ö±ĻßBC¾ąĄėŹĒ![]() £¬ĒóµćPµÄ×ų±ź£»
£¬ĒóµćPµÄ×ų±ź£»
£Ø3£©Į¬½ÓAP½»Ļ߶ĪBCÓŚµćH£¬µćMŹĒyÖįøŗ°ėÖįÉĻŅ»µć£¬ĒŅCH=BM£¬µ±AH+CMµÄÖµ×īŠ”Ź±£¬ĒėÖ±½ÓŠ“³öµćMµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
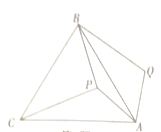
”¾ĢāÄæ”æČēĶ¼£¬![]() ŹĒµČ±ßČż½ĒŠĪ
ŹĒµČ±ßČż½ĒŠĪ![]() ÄŚŅ»µć£¬½«Ļ߶Ī
ÄŚŅ»µć£¬½«Ļ߶Ī![]() Čʵć
Čʵć![]() Ė³Ź±ÕėŠż×Ŗ
Ė³Ź±ÕėŠż×Ŗ![]() µĆµ½Ļ߶Ī
µĆµ½Ļ߶Ī![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £®Čō
£®Čō![]() £¬
£¬![]() £¬
£¬![]() £¬ŌņĖıߊĪ
£¬ŌņĖıߊĪ![]() µÄĆ껿ĪŖ£Ø £©
µÄĆ껿ĪŖ£Ø £©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ĖıߊĪABCDŹĒ¾ŲŠĪ£¬AD”ĪxÖį£¬A£Ø![]() £¬
£¬![]() £©£¬AB=1£¬AD=2£®
£©£¬AB=1£¬AD=2£®

£Ø1£©Ö±½ÓŠ“³öB”¢C”¢DČżµćµÄ×ų±ź£»
£Ø2£©½«¾ŲŠĪABCDĻņÓŅĘ½ŅĘmøöµ„Ī»£¬Ź¹µćA”¢CĒ”ŗĆĶ¬Ź±ĀäŌŚ·“±ČĄżŗÆŹż![]() £Ø
£Ø![]() £©µÄĶ¼ĻóÉĻ£¬µĆ¾ŲŠĪA”äB”äC”äD”䣮Ēó¾ŲŠĪABCDµÄĘ½ŅĘ¾ąĄėmŗĶ·“±ČĄżŗÆŹżµÄ½āĪöŹ½£®
£©µÄĶ¼ĻóÉĻ£¬µĆ¾ŲŠĪA”äB”äC”äD”䣮Ēó¾ŲŠĪABCDµÄĘ½ŅĘ¾ąĄėmŗĶ·“±ČĄżŗÆŹżµÄ½āĪöŹ½£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
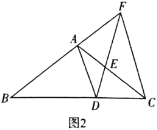
”¾ĢāÄæ”æČēĶ¼1£¬![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬
£¬![]() ĪŖ
ĪŖ![]() ÉĻŅ»¶Æµć£¬ĒŅ
ÉĻŅ»¶Æµć£¬ĒŅ![]() £¬
£¬![]() Óė
Óė![]() µÄŃÓ³¤Ļß½»ÓŚµć
µÄŃÓ³¤Ļß½»ÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £®
£®
£Ø1£©¢ŁĒóÖ¤£ŗ![]() £»
£»
¢ŚČō![]() £¬µ±
£¬µ±![]() Ź±£¬Ēó
Ź±£¬Ēó![]() µÄ³¤£»
µÄ³¤£»
£Ø2£©ČēĶ¼2£¬µ±![]() Ź±£¬ĒóÖ¤£ŗ
Ź±£¬ĒóÖ¤£ŗ![]() Ę½·Ö
Ę½·Ö![]() £®
£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĶõĄĻŹ¦“ÓѧŠ£³ö·¢£¬µ½¾ąŃ§Š£![]() µÄijÉĢ³”Č„øųѧɜĀņ½±Ę·£¬ĖūĻČ²½ŠŠĮĖ
µÄijÉĢ³”Č„øųѧɜĀņ½±Ę·£¬ĖūĻČ²½ŠŠĮĖ![]() ŗ󣬻»ĘļÉĻĮĖ¹²Ļķµ„³µ£¬µ½“ļÉĢ³”Ź±£¬Č«³Ģ×ܹ²øÕŗĆ»ØĮĖ
ŗ󣬻»ĘļÉĻĮĖ¹²Ļķµ„³µ£¬µ½“ļÉĢ³”Ź±£¬Č«³Ģ×ܹ²øÕŗĆ»ØĮĖ![]() .ŅŃÖŖĶõĄĻŹ¦Ęļ¹²Ļķµ„³µµÄĘ½¾łĖŁ¶ČŹĒ²½ŠŠĖŁ¶ČµÄ3±¶£Ø×Ŗ»»³öŠŠ·½Ź½Ź±£¬ĖłŠčŹ±¼äŗöĀŌ²»¼Ę£©.
.ŅŃÖŖĶõĄĻŹ¦Ęļ¹²Ļķµ„³µµÄĘ½¾łĖŁ¶ČŹĒ²½ŠŠĖŁ¶ČµÄ3±¶£Ø×Ŗ»»³öŠŠ·½Ź½Ź±£¬ĖłŠčŹ±¼äŗöĀŌ²»¼Ę£©.
£Ø1£©ĒóĶõĄĻŹ¦²½ŠŠŗĶĘļ¹²Ļķµ„³µµÄĘ½¾łĖŁ¶Č·Ö±šĪŖ¶ąÉŁ£æ
£Ø2£©ĀņĶź½±Ę·ŗó£¬ĶõĄĻŹ¦ŌĀ··µ»Ų£¬ĪŖ°“Ź±ÉĻ°ą£¬Ā·ÉĻĖł»ØŹ±¼ä×ī¶ąÖ»Ź£10·ÖÖÓ£¬ČōĶõĄĻŹ¦ČŌ²ÉČ”ĻČ²½ŠŠ£¬ŗó»»Ęļ¹²Ļķµ„³µµÄ·½Ź½·µ»Ų£¬ĪŹ£ŗĖū×ī¶ąæɲ½ŠŠ¶ąÉŁĆ×£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com