
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=BCЃЌжБЯпMNОЙ§ЕуCЃЌЧвADЁЭMNгкDЃЌBEЁЭMNгкEЃЎ
ЃЈ1ЃЉЕБжБЯпMNШЦЕуCа§зЊЕНЭМ1ЕФЮЛжУЪБЃЌЧѓжЄЃКЂйЁїADCЁеЁїCEBЃЛЂкDE=AD+BEЃЛ
ЃЈ2ЃЉЕБжБЯпMNШЦЕуCа§зЊЕНЭМ2ЕФЮЛжУЪБЃЌЧѓжЄЃКDE=ADЉBEЃЛ
ЃЈ3ЃЉЕБжБЯпMNШЦЕуCа§зЊЕНЭМ3ЕФЮЛжУЪБЃЌЪдЮЪDEЁЂADЁЂBEОпгадѕбљЕФЕШСПЙиЯЕЃПЧыаДГіетИіЕШСПЙиЯЕЃЌВЂМгвджЄУїЃЎ

ЁОД№АИЁПЃЈ1ЃЉЂйжЄУїМћНтЮіЃЛЂкжЄУїМћНтЮіЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉDE=BEЉADЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЭЌНЧЕФгрНЧЯрЕШЕУЕНЁЯACD=ЁЯCBEЃЌМДПЩжЄУїЁїADCЁеЁїCEBЃЛ
ЃЈ2ЃЉИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНAD=CEЃЌDC=EBЃЌМДПЩжЄУїDE=ADЉBEЃЛ
ЃЈ3ЃЉгыЃЈ1ЃЉЕФжЄУїЗНЗЈРрЫЦЃЌжЄЕФЁїADCЁеЁїCEBЃЌЕУГіAD=CEЃЌDC=EBЃЌМДПЩЕУГіDEЁЂADЁЂBEЕФЕШСПЙиМќ.
ЃЈ1ЃЉЁпЁЯACB=90Ёу
ЁрЁЯACD+ЁЯBCE=90Ёу
гжЁпADЁЭMNЃЌBEЁЭMN
ЁрЁЯADC=ЁЯCEB=90Ёу
ЁрЁЯBCE+ЁЯCBE=90Ёу
ЁрЁЯACD=ЁЯCBE
дкЁїADCКЭЁїCEBжаЃЌ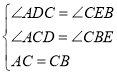
ЁрЁїADCЁеЁїCEB
ЁрAD=CEЃЌDC=BE
ЁрDE=DC+CE=BE+ADЃЛ
ЃЈ2ЃЉдкЁїADCКЭЁїCEBжаЃЌ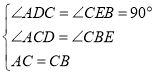
ЁрЁїADCЁеЁїCEB
ЁрAD=CEЃЌDC=EB
ЁрDE=CEЉDC=ADЉEBЃЛ
ЃЈ3ЃЉDE=BEЉADЃЎ
дкЁїADCКЭЁїCEBжаЃЌ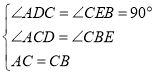
ЁрЁїADCЁеЁїCEB
ЁрAD=CEЃЌDC=BE
ЁрDE=DCЉCE=BEЉADЃЎ


 вЛБОКУЬтПкЫуЬтПЈЯЕСаД№АИ
вЛБОКУЬтПкЫуЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBAC=90ЁуЃЌADЪЧИпЃЌBEЪЧжаЯпЃЌCFЪЧНЧЦНЗжЯпЃЌCFНЛADгкЕуGЃЌНЛBEгкЕуHЃЌЯТУцЫЕЗЈжае§ШЗЕФађКХЪЧ_____ЃЎ
ЂйЁїABEЕФУцЛ§ЕШгкЁїBCEЕФУцЛ§ЃЛЂкЁЯAFG=ЁЯAGFЃЛЂлЁЯFAG=2ЁЯACFЃЛЂмBH=CHЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШчЭМЫљЪОЕФе§ЗНаЮЭјИёжаЃЌУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ЃЌИёЕуШ§НЧаЮЃЈЖЅЕуЪЧЭјИёЯпЕФНЛЕуЕФШ§НЧаЮЃЉABCЕФЖЅЕуAЃЌCЕФзјБъЗжБ№ЮЊЃЈЉ4ЃЌ5ЃЉЃЌЃЈЉ1ЃЌ3ЃЉЃЎ
ЃЈ1ЃЉЧыдкШчЭМЫљЪОЕФЭјИёЦНУцФкзїГіЦНУцжБНЧзјБъЯЕЃЛ
ЃЈ2ЃЉЧызїГіЁїABCЙигкyжсЖдГЦЕФЁїA1B1C1ЃЛ
ЃЈ3ЃЉаДГіЕуB1ЕФзјБъЃЛ
ЃЈ4ЃЉЧѓЁїABCЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтЯТСаИїЬтЃК
(1)ЯШЛЏМђЃЌдйЧѓДњЪ§ЪН(![]() ЕФжЕЃЌЦфжаxЃН
ЕФжЕЃЌЦфжаxЃН![]() cos30ЁуЃЋ
cos30ЁуЃЋ![]() ЃЛ
ЃЛ
(2)вбжЊІСЪЧШёНЧЃЌЧвsin(ІСЃЋ15Ёу)ЃН![]() .МЦЫу
.МЦЫу![]() Ѓ4cosІСЃ(ІаЃ3.14)0ЃЋtanІСЃЋ(
Ѓ4cosІСЃ(ІаЃ3.14)0ЃЋtanІСЃЋ(![]() )Ѓ1ЕФжЕЃЎ
)Ѓ1ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуBЁЂEЁЂCЁЂFдквЛЬѕжБЯпЩЯЃЌAB=DFЃЌAC=DEЃЌЁЯA=ЁЯDЃЎ
ЃЈ1ЃЉЧѓжЄЃКACЁЮDEЃЛ
ЃЈ2ЃЉШєBF=13ЃЌEC=5ЃЌЧѓBCЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁдёЪЪЕБЗНЗЈНтЯТСаЗНГЬЃК
(1) ![]()
(2) ![]()
(3) ![]()
(4) Ѓ![]() x2Ѓ3xЃЋ6ЃН0ЃЛ
x2Ѓ3xЃЋ6ЃН0ЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌЁЯA=60ЁуЃЌ ЁЯADC=ЁЯABC=90ЁуЃЌдкABЁЂADЩЯЗжБ№еввЛЕуFЁЂEЃЌСЌНгCEЁЂEFЁЂCFЃЌЕБЁїCEFЕФжмГЄзюаЁЪБЃЌдђЁЯECFЕФЖШЪ§ЮЊ______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃК
аЁУїгіЕНвЛИіЮЪЬтЃКдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Ш§БпЕФГЄЗжБ№ЮЊ
Ш§БпЕФГЄЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
аЁУїЪЧетбљНтОіЮЪЬтЕФЃКШчЭМЂйЫљЪОЃЌЯШЛвЛИіе§ЗНаЮЭјИёЃЈУПИіаЁе§ЗНаЮЕФБпГЄЮЊ![]() ЃЉЃЌдйдкЭјИёжаЛГіИёЕу
ЃЉЃЌдйдкЭјИёжаЛГіИёЕу![]() ЃЈМД
ЃЈМД![]() Ш§ИіЖЅЕуЖМдкаЁе§ЗНаЮЕФЖЅЕуДІЃЉЃЌДгЖјНшжњЭјИёОЭФмМЦЫуГі
Ш§ИіЖЅЕуЖМдкаЁе§ЗНаЮЕФЖЅЕуДІЃЉЃЌДгЖјНшжњЭјИёОЭФмМЦЫуГі![]() ЕФУцЛ§ЃЎЫћАбетжжНтОіЮЪЬтЕФЗНЗЈГЦЮЊЙЙЭМЗЈЃЎ
ЕФУцЛ§ЃЎЫћАбетжжНтОіЮЪЬтЕФЗНЗЈГЦЮЊЙЙЭМЗЈЃЎ
ВЮПМаЁУїНтОіЮЪЬтЕФЗНЗЈЃЌЭъГЩЯТСаЮЪЬтЃК
ЃЈ![]() ЃЉЭМ
ЃЉЭМ![]() ЪЧвЛИі
ЪЧвЛИі![]() ЕФе§ЗНаЮЭјИёЃЈУПИіаЁе§ЗНаЮЕФБпГЄЮЊ
ЕФе§ЗНаЮЭјИёЃЈУПИіаЁе§ЗНаЮЕФБпГЄЮЊ![]() ЃЉ ЃЎ
ЃЉ ЃЎ
ЂйРћгУЙЙЭМЗЈдкД№ОэЕФЭМ![]() жаЛГіШ§БпГЄЗжБ№ЮЊ
жаЛГіШ§БпГЄЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФИёЕу
ЕФИёЕу![]() ЃЎ
ЃЎ
ЂкМЦЫуЂйжа![]() ЕФУцЛ§ЮЊ__________ЃЎЃЈжБНгаДГіД№АИЃЉ
ЕФУцЛ§ЮЊ__________ЃЎЃЈжБНгаДГіД№АИЃЉ
ЃЈ![]() ЃЉШчЭМ
ЃЉШчЭМ![]() ЃЌвбжЊ
ЃЌвбжЊ![]() ЃЌвд
ЃЌвд![]() ЃЌ
ЃЌ![]() ЮЊБпЯђЭтзїе§ЗНаЮ
ЮЊБпЯђЭтзїе§ЗНаЮ![]() ЃЌ
ЃЌ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
ЂйХаЖЯ![]() гы
гы![]() УцЛ§жЎМфЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
УцЛ§жЎМфЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЂкШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌжБНгаДГіСљБпаЮ
ЃЌжБНгаДГіСљБпаЮ![]() ЕФУцЛ§ЮЊ__________ЃЎ
ЕФУцЛ§ЮЊ__________ЃЎ



ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋГЄЗНаЮжНЦЌABCDелЕўЃЌЪЙЕуCгыЕуAжиКЯЃЌелКлEFЗжБ№гыABЁЂDCНЛгкЕуEКЭЕуFЃЎ
ЃЈ1ЃЉжЄУїЃКЁїADFЁеЁїABЁфEЃЛ
ЃЈ2ЃЉШєAD=12ЃЌDC=18ЃЌЧѓЁїAEFЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com