
ЁОЬтФПЁПЁЖШчЙћЯыЛйЕєвЛИіКЂзгЃЌОЭИјЫћвЛВПЪжЛњ!ЁЗетЪЧЮЂаХХѓгбШІШШДЋЕФвЛЦЊЮФеТЃЎЙњМЪЩЯ,ЗЈЙњНЬг§ВПаћВМДг2018Фъ9дТаТбЇЦкЦ№ЃЌаЁбЇКЭГѕжаНћжЙбЇЩњЪЙгУЪжЛњЃЎЮЊСЫНтбЇЩњЪжЛњЪЙгУЧщПіЃЌФГбЇаЃПЊеЙСЫЁАЪжЛњАщЮвНЁПЕааЁБжїЬтЛюЖЏЃЌЫћУЧЫцЛњГщШЁВПЗжбЇЩњНјааЁАЪЙгУЪжЛњФПЕФЁБКЭЁАУПжмЪЙгУЪжЛњЕФЪБМфЁБЕФЮЪОэЕїВщ,ВЂЛцжЦГЩШчЭМЫљЪОЕФЭГМЦЭМЃЌвбжЊЁАВщзЪСЯЁБЕФШЫЪ§ЪЧ![]() ШЫЃЎ
ШЫЃЎ

ЧыФуИљОнвдЩЯаХЯЂНтД№ЯТСаЮЪЬт:
![]() ЧѓГіБОДЮЫцЛњГщШЁЕФбЇЩњЙВгаЖрЩйШЫЃЛ
ЧѓГіБОДЮЫцЛњГщШЁЕФбЇЩњЙВгаЖрЩйШЫЃЛ
![]() дкЩШаЮЭГМЦЭМжаЃЌЁАЭцгЮЯЗЁБЖдгІЕФАйЗжБШЮЊ______________ЃЌдВаФНЧЖШЪ§ЪЧ_______________ЖШЃЛ
дкЩШаЮЭГМЦЭМжаЃЌЁАЭцгЮЯЗЁБЖдгІЕФАйЗжБШЮЊ______________ЃЌдВаФНЧЖШЪ§ЪЧ_______________ЖШЃЛ
![]() ВЙШЋЬѕаЮЭГМЦЭМЃЛ
ВЙШЋЬѕаЮЭГМЦЭМЃЛ
![]() ИУаЃЙВгабЇЩњ
ИУаЃЙВгабЇЩњ![]() ШЫЃЌЙРМЦУПжмЪЙгУЪжЛњЪБМфдк
ШЫЃЌЙРМЦУПжмЪЙгУЪжЛњЪБМфдк![]() аЁЪБвдЩЯ(ВЛКЌ
аЁЪБвдЩЯ(ВЛКЌ![]() аЁЪБ)ЕФШЫЪ§ЃЎ
аЁЪБ)ЕФШЫЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ШЫЃЛЃЈ2ЃЉ35%ЃЌ126ЃЛЃЈ3ЃЉМћНтЮіЃЛЃЈ4ЃЉ1344ШЫ
ШЫЃЛЃЈ2ЃЉ35%ЃЌ126ЃЛЃЈ3ЃЉМћНтЮіЃЛЃЈ4ЃЉ1344ШЫ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнвбжЊЁАВщзЪСЯЁБЕФШЫЪ§ЪЧ40ШЫГ§вдЫљеМАйЗжБШЮЊ40%ЃЌМДПЩЕУЕНБОДЮЫцЛњГщШЁЕФбЇЩњзмШЫЪ§ЃЛ
ЃЈ2ЃЉгЩЩШаЮЭГМЦЭМЦфЫћЕФАйЗжБШЧѓГіЁАЭцгЮЯЗЁБЕФАйЗжБШЃЌдйГЫвд360МДПЩЕУЕНдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉЧѓГі3аЁЪБвдЩЯЕФШЫЪ§ЃЌВЙШЋЬѕаЮЭГМЦЭММДПЩЃЛ
ЃЈ4ЃЉгЩУПжмЪЙгУЪжЛњЪБМфдк2аЁЪБвдЩЯЃЈВЛКЌ2аЁЪБЃЉЕФАйЗжБШГЫвд2100МДПЩЕУЕННсЙћЃЎ
ЃЈ1ЃЉ![]() ШЫЃЛ
ШЫЃЛ
ЃЈ2ЃЉИљОнЬтвтЕУЃК1ЉЃЈ40%+18%+7%ЃЉЃН35%ЃЌ
дђЁАЭцгЮЯЗЁБЖдгІЕФдВаФНЧЖШЪ§ЪЧ360ЁуЁС35%ЃН126ЁуЃЌ
ЙЪД№АИЮЊЃК35%ЃЌ126ЃЛ
ЃЈ3ЃЉ3аЁЪБвдЩЯЕФШЫЪ§ЮЊ100ЉЃЈ2+16+18+32ЃЉЃН32ЃЈШЫЃЉЃЌ
ВЙШЋЭМаЮШчЯТЃК
 ЃЛ
ЃЛ
ЃЈ4ЃЉИљОнЬтвтЕУЃК2100ЁС![]() ЃН1344ЃЈШЫЃЉЃЌ
ЃН1344ЃЈШЫЃЉЃЌ
дђУПжмЪЙгУЪжЛњЪБМфдк2аЁЪБвдЩЯЃЈВЛКЌ2аЁЪБЃЉЕФШЫЪ§дМга1344ШЫЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкСНЕу
жсНЛгкСНЕу![]() КЭ
КЭ![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЖЏЕу
ЖЏЕу![]() би
би![]() ЕФБп
ЕФБп![]() вдУПУы
вдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШгЩЦ№Еу
ИіЕЅЮЛГЄЖШЕФЫйЖШгЩЦ№Еу![]() ЯђжеЕу
ЯђжеЕу![]() дЫЖЏЃЌЙ§Еу
дЫЖЏЃЌЙ§Еу![]() зї
зї![]() жсЕФДЙЯпЃЌНЛ
жсЕФДЙЯпЃЌНЛ![]() ЕФСэвЛБп
ЕФСэвЛБп![]() гкЕу
гкЕу![]() НЋ
НЋ![]() би
би![]() елЕўЃЌЪЙЕу
елЕўЃЌЪЙЕу![]() ТфдкЕу
ТфдкЕу![]() ДІЃЌЩшЕу
ДІЃЌЩшЕу![]() ЕФдЫЖЏЪБМфЮЊ
ЕФдЫЖЏЪБМфЮЊ![]() УыЃЎ
УыЃЎ

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉNЮЊХзЮяЯпЩЯЕФЕу(Еу![]() ВЛгыЕу
ВЛгыЕу![]() жиКЯ)ЧвТњзу
жиКЯ)ЧвТњзу![]() жБНгаДГі
жБНгаДГі![]() ЕуЕФзјБъЃЛ
ЕуЕФзјБъЃЛ
ЃЈ3ЃЉЪЧЗёДцдкФГвЛЪБПЬ![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕФУцЛ§зюДѓЃЌШєДцдкЃЌЧѓГі
ЕФУцЛ§зюДѓЃЌШєДцдкЃЌЧѓГі![]() ЕФжЕКЭзюДѓУцЛ§ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕКЭзюДѓУцЛ§ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧе§ЗНаЮЃЌЕуEЪЧБпBCЕФжаЕуЃЌЁЯAEFЃН90ЁуЃЌЧвEFНЛе§ЗНаЮЭтНЧЕФЦНЗжЯпCFгкЕуFЃЎ

ЃЈ1ЃЉЧѓжЄЃКAEЃНEFЃЎ
ЃЈ2ЃЉЃЈЬНОП1ЃЉБфЬиЪтЮЊвЛАуЃКШєЬтжаЁАЕуEЪЧБпBCЕФжаЕуЁББфЮЊЁАЕуEЪЧBCБпЩЯШЮвтвЛЕуЁБЃЌдђЩЯЪіНсТлЪЧЗёШдШЛГЩСЂЃПЃЈЬюЁАЪЧЁБЛђЁАЗёЁБЃЉЃЎ
ЃЈ3ЃЉЃЈЬНОП2ЃЉдкЬНОП1ЕФЧАЬсЯТЃЌШєЬтжаНсТлЁАAEЃНEFЁБгыЬѕМўЁАCFЪЧе§ЗНаЮЭтНЧЕФЦНЗжЯпЁБЛЅЛЛЃЌдђУќЬтЪЧЗёЛЙГЩСЂЃПЧыИјГіжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЩфЯпABЩЯЫГДЮШЁСНЕуCЃЌDЃЌЪЙAC=CD=1ЃЌвдCDЮЊБпзїОиаЮCDEFЃЌDE=2ЃЌНЋЩфЯпABШЦЕуAбиФцЪБеыЗНЯђа§зЊЃЌа§зЊНЧМЧЮЊІСЃЈЦфжа0ЁуЃМІСЃМ45ЁуЃЉЃЌа§зЊКѓМЧзїЩфЯпABЁфЃЌЩфЯпABЁфЗжБ№НЛОиаЮCDEFЕФБпCFЃЌDEгкЕуGЃЌHЃЎШєCG=xЃЌEH=yЃЌдђЯТСаКЏЪ§ЭМЯѓжаЃЌФмЗДгГyгыxжЎМфЙиЯЕЕФЪЧЃЈ ЃЉ
A.
B.
C.
D.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгЩМИИіЯрЭЌЕФБпГЄЮЊ1ЕФаЁСЂЗНПщДюГЩЕФМИКЮЬхЕФИЉЪгЭМШчЯТЭМЃЌИёжаЕФЪ§зжБэЪОИУЮЛжУЕФаЁСЂЗНПщЕФИіЪ§ЃЎ
(1)ЧыдкЯТУцЗНИёжНжаЗжБ№ЛГіетИіЯђКЮЬхЕФжїЪгЭМКЭзѓЪгЭМЃЎ

(2)ИљОнШ§ЪгЭМЃЛетИізщКЯМИКЮЬхЕФБэУцЛ§ЮЊЁЁ_________ЁЁИіЦНЗНЕЅЮЛЃЎ(АќРЈЕзУцЛ§)
(3)ШєЩЯЪіаЁСЂЗНПщДюГЩЕФМИКЮЬхЕФИЉЪгЭМВЛБфЃЌИїЮЛжУЕФаЁСЂЗНПщИіЪ§ПЩвдИФБф(змЪ§ФПВЛБф)ЃЌдђДюГЩетбљЕФзщКЯМИКЮЬхжаЕФБэУцЛ§зюДѓЪЧЮЊЁЁ_________ЁЁИіЦНЗНЕЅЮЛЃЎ(АќРЈЕзУцЛ§)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACB=90ЁуЃЌOЪЧБпACЩЯвЛЕуЃЌвдOЮЊдВаФЃЌOAЮЊАыОЖЕФдВЗжБ№НЛABЃЌACгкЕуEЃЌDЃЌдкBCЕФбгГЄЯпЩЯШЁЕуFЃЌЪЙЕУBF=EFЃЌEFгыACНЛгкЕуGЃЎ
ЃЈ1ЃЉЪдХаЖЯжБЯпEFгыЁбOЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєOA=2ЃЌЁЯA=30ЁуЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпy=ax2Љ2x+cЕФЖдГЦжсЮЊжБЯпx=Љ1ЃЌЖЅЕуЮЊAЃЌгыyжсе§АыжсНЛЕуЮЊBЃЌЧвЁїABOЕФУцЛ§ЮЊ1ЃЎ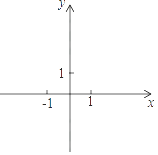
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉШєЕуPдкxжсЩЯЃЌЧвPA=PBЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЁЂ
ЁЂ![]() ЪЧЖдНЧЯп
ЪЧЖдНЧЯп![]() ЩЯЕФСНЕуЧв
ЩЯЕФСНЕуЧв![]() ЃЌЯТСаЫЕЗЈжае§ШЗЕФЪЧЃЈ ЃЉ
ЃЌЯТСаЫЕЗЈжае§ШЗЕФЪЧЃЈ ЃЉ
Ђй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂмЫФБпаЮ
ЃЛЂмЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЃЛЂн
ЮЊЦНааЫФБпаЮЃЛЂн![]() ЃЛЂо
ЃЛЂо![]() ЃЎ
ЃЎ

A.ЂйЂоB.ЂйЂкЂмЂоC.ЂйЂкЂлЂмD.ЂйЂкЂмЂнЂо
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§ ![]() ЕФЭМЯѓОЙ§A(2ЃЌ0)ЃЌBЃЈ0ЃЌ-6ЃЉСНЕу.
ЕФЭМЯѓОЙ§A(2ЃЌ0)ЃЌBЃЈ0ЃЌ-6ЃЉСНЕу.
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФНтЮіЪНМАЖЅЕузјБъЃЛ
ЃЈ2ЃЉЩшИУЖўДЮКЏЪ§ЕФЖдГЦжсгыxжсНЛгкЕуCЃЌСЌНгBAЃЌBCЃЌЧѓЁїABCЕФУцЛ§.
ЃЈ3ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдквЛЕуPЃЎЪЙЕУвдOЁЂBЁЂCЁЂPЫФЕуЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіPЕузјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com