选做题:已知二次函数y=ax2-ax+m的图象交x轴于A(x1,0)、B(x2,0)两点,x1<x2,交y轴的负半轴于C点,且AB=3,tan∠BAC-tan∠ABC=1.
(1)求此二次函数的解析式;
(2)在第一象限,抛物线上是否存在点P,使S△PAC=6?若存在,请你求出点P的坐标;不存在,说明理由.
【答案】
分析:(1)由二次函数y=ax
2-ax+m的图象交x轴于A(x
1,0)、B(x
2,0)两点,可知是ax
2-ax+m=0的两个根,得出两根之和;由AB=3,得出两根之差,求得x
1、x
2,根据tan∠BAC-tan∠ABC=1求得点C,解决问题;
(2)由P作AC的平行线EF,与y轴交于E,与x轴交于F,利用三角形的面积求得两点坐标,进一步求出直线EF,直线EF与抛物线在第一象限的交点就是P的坐标.
解答: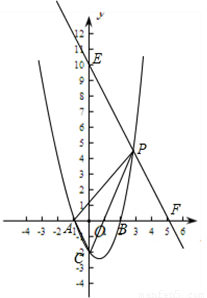
解:(1)由已知,有
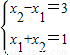
解得x
1=-1,x
2=2.
x
1x
2=-2=
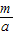
,
由已知三角函数关系知
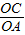
-
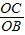
=1,
即
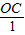
-
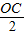
=1,得OC=2,
∴截距m=-2,
则a=1
∴y=x
2-x-2.
(2)存在.
过点P作AC的平行线,与y轴交于E,与x轴交于F.
由S
△PAC=S
△EAC=S
△FAC=6,
求得E(0,10),F(5,0),
得到直线EF的解析式为y=-2x+10,
解-2x+10=x
2-x-2,
可得x
1=-4,x
2=3,
于是P点的坐标为P
1(3,4),P
2(-4,18),
因为P点的坐标在第一象限,
所以P点的坐标为P(3,4).
点评:此题是一个综合性很强的题目,考查了一元二次方程根与系数的关系、三角函数、待定系数法求二次函数、及方程与函数之间的关系等,渗透数形结合的思想.

 解:(1)由已知,有
解:(1)由已知,有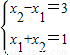
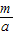 ,
,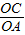 -
-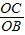 =1,
=1,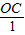 -
-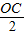 =1,得OC=2,
=1,得OC=2,
