
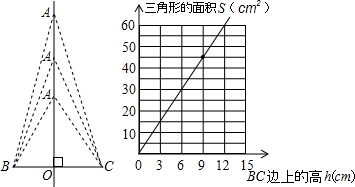
 下图表示了这钟变化规律.根据下面两个图回答问题:
下图表示了这钟变化规律.根据下面两个图回答问题: ×BC×h=
×BC×h= BC×9=45,
BC×9=45,

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
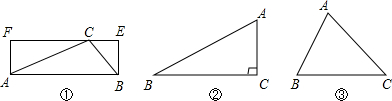
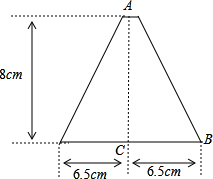 某家具市场现有大批如图所示的边角余料(单位:cm),采荷中学数学兴趣小组决定将其加工成等腰三角形,且满足以下两个要求:(1)三角形中至少有一边长为10cm;(2)三角形中至少有一边上的高为8cm.请给出三种不同的方案,标上相关线段的长度,并求出相应等腰三角形的面积(不需尺规作图).
某家具市场现有大批如图所示的边角余料(单位:cm),采荷中学数学兴趣小组决定将其加工成等腰三角形,且满足以下两个要求:(1)三角形中至少有一边长为10cm;(2)三角形中至少有一边上的高为8cm.请给出三种不同的方案,标上相关线段的长度,并求出相应等腰三角形的面积(不需尺规作图).查看答案和解析>>
科目:初中数学 来源: 题型:
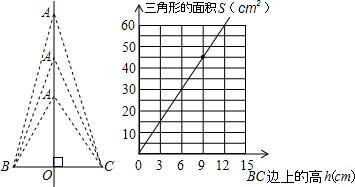 下图表示了这钟变化规律.根据下面两个图回答问题:
下图表示了这钟变化规律.根据下面两个图回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com