
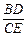 的值;
的值;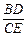 的值;
的值;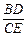 的取值范围(直接写出结论,不必证明),并探究
的取值范围(直接写出结论,不必证明),并探究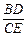 的
的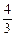 吗?若能,求出满足条件的D点的位置;若不能,说明理由
吗?若能,求出满足条件的D点的位置;若不能,说明理由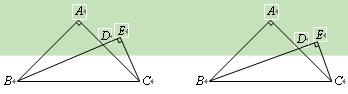
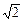 ,AD = 1-x.
,AD = 1-x.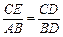 ,即
,即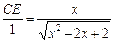 ,从而
,从而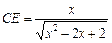 ,
,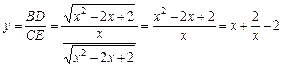 ,0<x<1,
,0<x<1,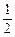 ,得
,得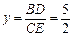 .
.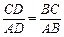 ,得
,得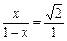 ,解得
,解得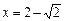 ,
,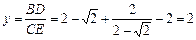 .
.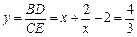 ,则有 3x2-10x + 6 = 0,解得
,则有 3x2-10x + 6 = 0,解得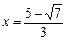 ∈(0,1),
∈(0,1),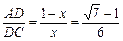 ,表明随着点D从A向C移动时,BD逐渐增大,而CE逐渐减小,的值则随着D从A向C移动而逐渐增大.
,表明随着点D从A向C移动时,BD逐渐增大,而CE逐渐减小,的值则随着D从A向C移动而逐渐增大.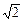 ,∠CBE = 45°-a.
,∠CBE = 45°-a.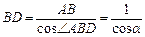 ;
;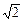 sin(45°-a).
sin(45°-a).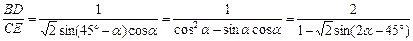 .下略……
.下略…… .
.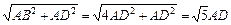 .
.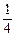 CE2 = CD2,于是
CE2 = CD2,于是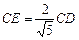 .
.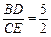 .
.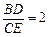 .
.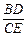 的值的取值范围为
的值的取值范围为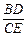 ≥1.下略……解析:
≥1.下略……解析:

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 3 |
| 3 |
| 5 |
2-2
|
2-2
|
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.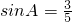 ,其中A为锐角,试求sadA的值;
,其中A为锐角,试求sadA的值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com