
ЁОЬтФПЁПЖЈвхЃКСНЬѕГЄЖШЯрЕШЃЌЧвЫќУЧЫљдкЕФжБЯпЛЅЯрДЙжБЕФЯпЖЮЃЌЮвУЧГЦЦфЛЅЮЊЁАЕШДЙЯпЖЮЁБЃЎ
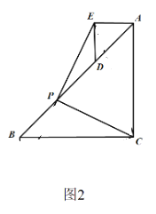
жЊЪЖгІгУЃКдкЁїABCКЭЁїADEжаЃЌAC=BCЃЌAE=DEЃЌЧвAE<ACЃЌ ЁЯACB=ЁЯAED=90ЁуЃЌСЌНгBDЃЌЕуPЪЧЯпЖЮBDЕФжаЕуЃЌСЌНгPCЃЌPEЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБAEдкЯпЖЮACЩЯЪБЃЌЯпЖЮPCгыЯпЖЮPEЪЧЗёЛЅЮЊЁАЕШДЙЯпЖЮЁБЃПЧыЫЕУїРэгЩЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌНЋЭМ1жаЕФЁїADEШЦЕуAЫГЪБеыа§зЊ90ЁуЃЌЕуDТфдкABБпЩЯЃЌЧыЫЕУїЯпЖЮPCгыЯпЖЮPEЛЅЮЊЁАЕШДЙЯпЖЮЁБЃЎ
ЭиеЙбгЩьЃКЃЈ3ЃЉНЋЭМ1жаЕФЁїADEШЦЕуAЫГЪБеыа§зЊ150ЁуЃЌШєBC=3ЃЌDE=1ЃЌЧѓPCЕФжЕЃЎ

ЁОД№АИЁПЃЈ1ЃЉЯпЖЮPCгыЯпЖЮPEЛЅЮЊЁАЕШДЙЯпЖЮЁБЃЌРэгЩМћНтЮіЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉбгГЄEPНЛBCгкЕуFЃЌЪзЯШжЄУї![]() ЃЌдђгаPF=PE=
ЃЌдђгаPF=PE=![]() EFЃЌBF=DEЃЌШЛКѓжЄУїЁїEFCЪЧЕШбќжБНЧШ§НЧаЮЃЌдйРћгУЕШбќжБНЧШ§НЧаЮЕФаджЪМДПЩжЄУїЯпЖЮPCгыЯпЖЮPEЛЅЮЊЁАЕШДЙЯпЖЮЁБЃЛ
EFЃЌBF=DEЃЌШЛКѓжЄУїЁїEFCЪЧЕШбќжБНЧШ§НЧаЮЃЌдйРћгУЕШбќжБНЧШ§НЧаЮЕФаджЪМДПЩжЄУїЯпЖЮPCгыЯпЖЮPEЛЅЮЊЁАЕШДЙЯпЖЮЁБЃЛ
ЃЈ2ЃЉзїBF//DEЃЌНЛEPЕФбгГЄЯпгкЕуFЃЌСЌНгCEЃЌCFЃЌЪзЯШжЄУї![]() ЃЌдђгаBF= DEЃЌ PE=PF=
ЃЌдђгаBF= DEЃЌ PE=PF=![]() EFЃЌШЛКѓРћгУЦНааЯпЕФаджЪЕУГіЁЯCBF=ЁЯCAEЃЌНјЖјПЩжЄ
EFЃЌШЛКѓРћгУЦНааЯпЕФаджЪЕУГіЁЯCBF=ЁЯCAEЃЌНјЖјПЩжЄ![]() ЃЌдђгаCF=CEЃЌЁЯFCB=ЁЯECAЃЌДгЖјЕУГіЁїFCEЪЧЕШбќжБНЧШ§НЧаЮЃЌдђНсТлПЩжЄЃЛ
ЃЌдђгаCF=CEЃЌЁЯFCB=ЁЯECAЃЌДгЖјЕУГіЁїFCEЪЧЕШбќжБНЧШ§НЧаЮЃЌдђНсТлПЩжЄЃЛ
ЃЈ3ЃЉзїBF//DEЃЌНЛEPЕФбгГЄЯпгкЕуFЃЌСЌНгCEЃЌCFЃЌЙ§ЕуEзїEHЁЭACНЛCAЕФбгГЄЯпгкЕуHЃЌЪзЯШжЄУї![]() ЃЌдђгаBF= DEЃЌ PE=PF=
ЃЌдђгаBF= DEЃЌ PE=PF=![]() EFЃЌШЛКѓПЩжЄ
EFЃЌШЛКѓПЩжЄ![]() ЃЌдђгаCF=CEЃЌЁЯFCB=ЁЯECAЃЌДгЖјЕУГіЁїFCEЪЧЕШбќжБНЧШ§НЧаЮЃЌдђPC=PE=
ЃЌдђгаCF=CEЃЌЁЯFCB=ЁЯECAЃЌДгЖјЕУГіЁїFCEЪЧЕШбќжБНЧШ§НЧаЮЃЌдђPC=PE=![]() ECЃЌШЛКѓдкRt
ECЃЌШЛКѓдкRt![]() AHEжаЃЌЧѓГіHE,AHЕФГЄЖШЃЌНјЖјЧѓГіCHЕФГЄЖШЃЌШЛКѓдкRt
AHEжаЃЌЧѓГіHE,AHЕФГЄЖШЃЌНјЖјЧѓГіCHЕФГЄЖШЃЌШЛКѓдкRt![]() CEHжаЃЌгЩЙДЙЩЖЈРэЧѓГіECЕФГЄЖШЃЌдђPCЕФГЄЖШПЩЧѓ ЃЎ
CEHжаЃЌгЩЙДЙЩЖЈРэЧѓГіECЕФГЄЖШЃЌдђPCЕФГЄЖШПЩЧѓ ЃЎ
НтЃК(1)ЯпЖЮPCгыЯпЖЮPEЛЅЮЊЁАЕШДЙЯпЖЮЁБЃЎ
РэгЩЃКШчЭМ1ЃЌбгГЄEPНЛBCгкЕуFЃЎ
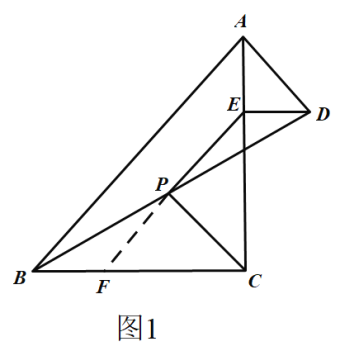
ЁпЁЯACB=ЁЯAED=90ЁуЃЌ
ЁрDE![]() BCЃЌ
BCЃЌ
ЁрЁЯEDP=ЁЯFBPЃЎ
ЁпЕуPЪЧЯпЖЮBDЕФжаЕуЃЌ
ЁрPB=PDЃЎ
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ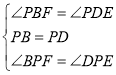
![]()
ЁрPF=PE=![]() EFЃЌBF=DEЃЎ
EFЃЌBF=DEЃЎ
ЁпAC=BCЃЌAE=DEЃЌ
ЁрACЉAE=BCЉBFЃЌМДEC=FCЃЎ
гжЁпЁЯACB=90ЁуЃЌ
ЁрЁїEFCЪЧЕШбќжБНЧШ§НЧаЮЃЎ
ЁпEP=FPЃЌ
ЁрPC=PEЃЌPCЁЭPEЃЌ
ЁрЯпЖЮPCгыЯпЖЮPEЛЅЮЊЁАЕШДЙЯпЖЮЁБЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌзїBF//DEЃЌНЛEPЕФбгГЄЯпгкЕуFЃЌСЌНгCEЃЌCFЃЌ
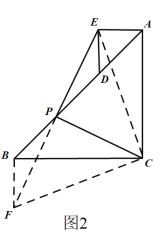
ЁпDE![]() BFЃЌ
BFЃЌ
ЁрЁЯEDP=ЁЯFBPЃЎ
ЁпЕуPЪЧЯпЖЮBDЕФжаЕуЃЌ
ЁрPB=PDЃЎ
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ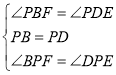
![]()
ЁрBF= DEЃЌ PE=PF=![]() EFЃЎ
EFЃЎ
ЁпDE=AEЃЌ
ЁрBF=AEЃЎ
ЁпЁЯCAE=90ЁуЃЌЁЯAED=90ЁуЃЌ
ЁрED![]() ACЃЎ
ACЃЎ
![]() ЃЌ
ЃЌ
ЁрFB![]() ACЃЌ
ACЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЁЯCBF=ЁЯCAEЃЎ
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
![]()
ЁрCF=CEЃЌЁЯFCB=ЁЯECAЃЎ
ЁпЁЯACB=90ЁуЃЌ
ЁрЁЯFCE=90ЁуЃЌ
ЁрЁїFCEЪЧЕШбќжБНЧШ§НЧаЮЃЎ
ЁпPE=PFЃЌ
ЁрPCЁЭPEЃЌPC=PEЃЌ
ЁрЯпЖЮPCгыЯпЖЮPEЛЅЮЊЁАЕШДЙЯпЖЮЁБЃЛ
(3)ШчЭМ3
зїBF//DEЃЌНЛEPЕФбгГЄЯпгкЕуFЃЌСЌНгCEЃЌCFЃЌЙ§ЕуEзїEHЁЭACНЛ
ЕБа§зЊНЧЮЊ150ЁуЪБЃЌгЩа§зЊПЩжЊЃЌЁЯCAE=150ЁуЃЌDEгыBCЫљМаЕФШёНЧЮЊ30ЁуЃЌ
ЁрЁЯFBC=ЁЯEAC=150ЁуЃЎ
ЁпDE![]() BFЃЌ
BFЃЌ
ЁрЁЯEDP=ЁЯFBPЃЎ
ЁпЕуPЪЧЯпЖЮBDЕФжаЕуЃЌ
ЁрPB=PDЃЎ
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
![]()
ЁрBF= DEЃЌ PE=PF=![]() EFЃЎ
EFЃЎ
ЁпDE=AE ЃЌ
ЁрBF=AEЃЎ
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ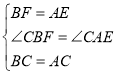
![]()
ЁрCF=CEЃЌЁЯFCB=ЁЯECAЃЎ
ЁпЁЯACB=90Ёу ЃЌ
ЁрЁЯFCE=90ЁуЃЌ
ЁрЁїFCEЪЧЕШбќжБНЧШ§НЧаЮЃЎ
ЁпPE=PFЃЌ
ЁрPCЁЭPEЃЌPC=PE=![]() ECЃЎ
ECЃЎ
дкRt![]() AHEжаЃЌЁЯEAH=30ЁуЃЌAE=DE=1ЃЌ
AHEжаЃЌЁЯEAH=30ЁуЃЌAE=DE=1ЃЌ
ЁрHE=![]() ЃЌAH=
ЃЌAH=![]() ЃЎ
ЃЎ
гжЁпAC=BC=3ЃЌ
ЁрCH=AC+AH=3+![]() ЃЎ
ЃЎ
дкRt![]() CEHжаЃЌ
CEHжаЃЌ
гЩЙДЙЩЖЈРэЕУ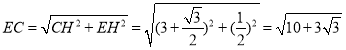 ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ


 УћЪІН№ЪжжИСьЯЮПЮЪБЯЕСаД№АИ
УћЪІН№ЪжжИСьЯЮПЮЪБЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ![]() ЃЎ Еу
ЃЎ Еу![]() ЪЧЦНУцФкВЛгыЕу
ЪЧЦНУцФкВЛгыЕу![]() жиКЯЕФШЮвтвЛЕуЃЌ СЌНг
жиКЯЕФШЮвтвЛЕуЃЌ СЌНг![]() ЃЌНЋЯпЖЮ
ЃЌНЋЯпЖЮ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЕУЕНЯпЖЮ
ЕУЕНЯпЖЮ![]() ЃЌСЌНг
ЃЌСЌНг![]()
ЃЈ1ЃЉЖЏЪжВйзї
ШчЭМ1ЃЌЕБ![]() ЪБЃЌЮвУЧЭЈЙ§гУ ПЬЖШГпКЭСПНЧЦїЖШСПЗЂЯжЃК
ЪБЃЌЮвУЧЭЈЙ§гУ ПЬЖШГпКЭСПНЧЦїЖШСПЗЂЯжЃК
![]() ЕФжЕЪЧ
ЕФжЕЪЧ![]() ЃЛжБЯп
ЃЛжБЯп![]() гыжБЯп
гыжБЯп![]() ЯрНЛЫљГЩЕФНЯаЁНЧЕФЖШЪ§ЪЧ
ЯрНЛЫљГЩЕФНЯаЁНЧЕФЖШЪ§ЪЧ![]() ЃЛ
ЃЛ
ЧыжЄУївдЩЯНсТле§ШЗЃЎ
ЃЈ2ЃЉРрБШЬНОП
ШчЭМ2ЃЌЕБ![]() ЪБЃЌЧыаДГі
ЪБЃЌЧыаДГі![]() ЕФжЕМАжБЯп
ЕФжЕМАжБЯп![]() гыжБЯп
гыжБЯп![]() ЯрНЛЫљГЩЕФНЯаЁНЧЕФЖШЪ§ЃЌВЂОЭЭМ2ЕФЧщаЮЫЕУїРэгЩЃЎ
ЯрНЛЫљГЩЕФНЯаЁНЧЕФЖШЪ§ЃЌВЂОЭЭМ2ЕФЧщаЮЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЦЗдМлЮЊ100дЊЃЌЕквЛДЮеЧМл![]() ЃЌЕкЖўДЮдкЕквЛДЮЕФЛљДЁЩЯгжеЧМл
ЃЌЕкЖўДЮдкЕквЛДЮЕФЛљДЁЩЯгжеЧМл![]() ЃЌЩшЦНОљУПДЮдіГЄЕФАйЗжЪ§ЮЊxЃЌФЧУДxгІТњзуЕФЗНГЬЪЧ
ЃЌЩшЦНОљУПДЮдіГЄЕФАйЗжЪ§ЮЊxЃЌФЧУДxгІТњзуЕФЗНГЬЪЧ![]() ЁЁЁЁ
ЁЁЁЁ![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧОиаЮЃЌАбОиаЮбиACелЕўЃЌЕуBТфдкЕуEДІЃЌAEгыDCЕФНЛЕуЮЊOЃЌСЌНгDEЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїADEЁеЁїCEDЃЛ
ЃЈ2ЃЉЧѓжЄЃКDEЁЮACЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫгНгЬхг§жаПМЃЌФГаЃОХЃЈ1ЃЉАрЕФЬхг§РЯЪІЖдШЋАр45УћбЇЩњНјааСЫвЛДЮЬхг§ФЃФтВтЪд(ЕУЗжОљЮЊећЪ§)ЃЌГЩМЈТњЗжЮЊ10ЗжЃЌИУАрЕФЬхг§ЮЏдБИљОнетДЮВтЪдГЩМЈЃЌжЦзїСЫЭГМЦЭМКЭЗжЮіБэШчЯТЃК
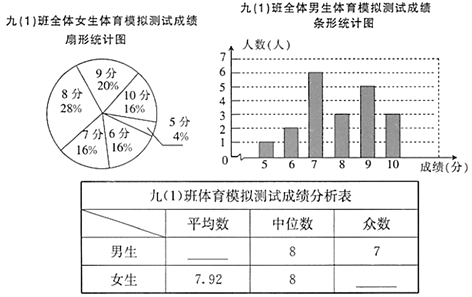
ИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃЎ
ЃЈ1ЃЉетИіАрЙВгаФаЩњ_________ШЫЃЌХЎЩњга____________ШЫЃЎ
ЃЈ2ЃЉЧыФуВЙШЋОХ(1)АрЬхг§ФЃФтВтЪдГЩМЈЗжЮіБэЃЎ
ЃЈ3ЃЉФуШЯЮЊдкетДЮЬхг§ФЃФтВтЪджаЃЌОХЃЈ1ЃЉАрЕФШЋЬхФаЩњКЭШЋЬхХЎЩњЃЌЫЕФБэЯжИќКУвЛаЉЃПЧыаДГівЛЬѕжЇГжФуЕФПДЗЈЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЖдМДНЋВЮМгжаПМЕФ4000УћГѕжаБЯвЕЩњНјааСЫвЛДЮЪгСІГщбљЕїВщЃЌЛцжЦГіЦЕЪ§ЗжВМБэКЭВЛЭъећЕФЦЕЪ§ЗжВМжБЗНЭМЃЎЧыИљОнЭМБэаХЯЂЛиД№ЯТСаЮЪЬтЃК
ГѕжаБЯвЕЩњЪгСІГщбљЕїВщЦЕЪ§ЗжВМБэ
ЪгСІ | ЦЕЪ§ЃЈШЫЃЉ | ЦЕТЪ |
4.0ЁмxЃМ4.3 | 20 | 0.1 |
4.3ЁмxЃМ4.6 | 40 | 0.2 |
4.6ЁмxЃМ4.9 | 70 | 0.35 |
4.9ЁмxЃМ5.2 | a | 0.3 |
5.2ЁмxЃМ5.5 | 10 | b |

ЃЈ1ЃЉБОДЮЕїВщбљБОШнСПЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉдкЦЕЪ§ЗжВМБэжаЃЌaЃН ЁЁЃЌbЃНЁЁ ЁЁЃЌВЂНЋЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉШєЪгСІдк4.9вдЩЯЃЈКЌ4.9ЃЉОљЪєБъзМЪгСІЃЌИљОнЩЯЪіаХЯЂЙРМЦШЋЧјГѕжаБЯвЕЩњжаДяЕНБъзМЪгСІЕФбЇЩњдМгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊМЄЗЂбЇЩњЕФдФЖСаЫШЄЃЌХрбјбЇЩњСМКУЕФдФЖСЯАЙпЃЌЮвЧјФГаЃгћЙКНјвЛХњбЇЩњЯВЛЖЕФЭМЪщЃЌбЇаЃзщжЏбЇЩњЛсЫцЛњГщШЁВПЗжбЇЩњНјааЮЪОэЕїВщЃЌБЛЕїВщбЇЩњаыДгЁАЮФЪЗРрЁЂЩчПЦРрЁЂаЁЫЕРрЁЂЩњЛюРрЁБжабЁдёздМКЯВЛЖЕФвЛРрЃЌИљОнЕїВщНсЙћЛцжЦСЫЭГМЦЭМЃЈЮДЭъГЩЃЉЃЌЧыИљОнЭМжааХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЬюПеЛђбЁдёЃКДЫДЮЙВЕїВщСЫ______УћбЇЩњЃЛЭМ2жаЁАаЁЫЕРрЁБЫљдкЩШаЮЕФдВаФНЧЮЊ______ЖШЃЛбЇЩњЛсВЩгУЕФЕїВщЗНЪНЪЧ______ЃЎAЃЎЦеВщ BЃЎГщбљЕїВщ
ЃЈ2ЃЉНЋЬѕаЮЭГМЦЭМЃЈЭМ1ЃЉВЙГфЭъећЃЛ
ЃЈ3ЃЉШєИУаЃЙВгабЇЩњ2500ШЫЃЌЪдЙРМЦИУаЃЯВЛЖЁАЩчПЦРрЁБЪщМЎЕФбЇЩњШЫЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ xOy жаЃЌНЋЕу AЃЈ2ЃЌ4ЃЉЯђЯТЦНвЦ 2 ИіЕЅЮЛЕУЕНЕу CЃЌЗДБШР§КЏЪ§y ![]() (mЁй0)ЕФЭМЯѓОЙ§Еу CЃЌЙ§Еу C зї CBЁЭx жсгкЕу B
(mЁй0)ЕФЭМЯѓОЙ§Еу CЃЌЙ§Еу C зї CBЁЭx жсгкЕу B

ЃЈ1ЃЉЧѓ m ЕФжЕЃЛ
ЃЈ2ЃЉвЛДЮКЏЪ§ y=kx+b(k<0)ЕФЭМЯѓОЙ§Еу CЃЌНЛ x жсгкЕу DЃЌ ЯпЖЮ CDЃЌBDЃЌBC ЮЇГЩЕФЧјгђЃЈВЛКЌБпНчЃЉЮЊ GЃЛ ШєКсЁЂзнзјБъЖМЪЧећЪ§ЕФЕуНазіећЕу
Ђйb=3 ЪБЃЌжБНгаДГіЧјгђ G ФкЕФећЕуИіЪ§
ЂкШєЧјгђ G ФкУЛгаећЕуЃЌНсКЯКЏЪ§ЭМЯѓЃЌШЗЖЈ k ЕФШЁжЕЗЖЮЇ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖделОиаЮжНЦЌABCDЃЌЪЙADгыBCжиКЯЃЌЕУЕНелКлEFЃЌАбжНЦЌеЙЦНЃЌдйвЛДЮелЕўжНЦЌЃЌЪЙЕуAТфдкEFЩЯЕФЕуAЁфДІЃЌВЂЪЙелКлОЙ§ЕуBЃЌЕУЕНелКлBMЃЌШєОиаЮжНЦЌЕФПэAB=4ЃЌдђелКлBMЕФГЄЮЊ( )
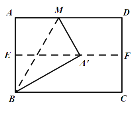
A.![]() B.
B.![]() C.8D.
C.8D.![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com