
【题目】下列命题中:①等腰三角形底边的中点到两腰的距离相等;②等腰三角形的高、中线、角平分线互相重合; ③若![]() 与
与![]() 成轴对称,则
成轴对称,则![]() 一定与
一定与![]() 全等;④有一个角是
全等;④有一个角是![]() 度的三角形是等边三角形;⑤等腰三角形的对称轴是顶角的平分线.正确命题的个数是( )
度的三角形是等边三角形;⑤等腰三角形的对称轴是顶角的平分线.正确命题的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=40°,则∠CDE的度数为( )
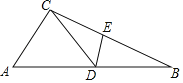
A.50°B.40°C.60°D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+3分别与x,y轴交于点N,M,与反比例函数y= ![]() (x>0)的图象交于点A,若AM:MN=2:3,则k=________.
(x>0)的图象交于点A,若AM:MN=2:3,则k=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OB,AB⊥x轴于C,点A(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图象上.
的图象上.
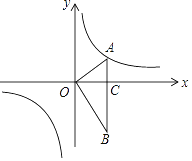
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)在x轴上存在一点P,使S△AOP= ![]() S△AOB, 求点P的坐标.
S△AOB, 求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
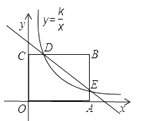
【题目】如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且点B(4,3),反比例函数y=![]() 图象与BC交于点D,与AB交于点E,其中D(1,3).
图象与BC交于点D,与AB交于点E,其中D(1,3).
(1)求反比例函数的解析式及E点的坐标;
(2)求直线DE的解析式;
(3)若矩形OABC对角线的交点为F (2,![]() ),作FG⊥x轴交直线DE于点G.
),作FG⊥x轴交直线DE于点G.
①请判断点F是否在此反比例函数y=![]() 的图象上,并说明理由;
的图象上,并说明理由;
②求FG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
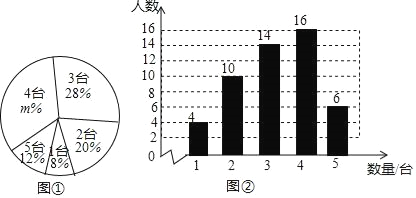
【题目】随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)求本次调查获取的样本数据的众数、中位数和平均数;
(3)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
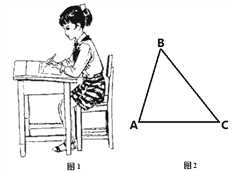
【题目】人写字时眼睛和笔端的距离超过30cm时则符合保护视力的要求.图1是一位同学的坐姿,把她的眼睛B、肘关节C和笔端A的位置关系抽象成图2的△ABC,BC=30cm,AC=22cm,∠ACB=530,她的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin530≈0.8,cos530≈0.6,tan530≈1.3)
查看答案和解析>>
科目:初中数学 来源: 题型:
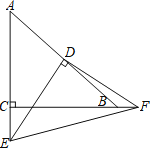
【题目】如图,已知Rt △ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC、CB的延长线于E、F.下面结论一定成立的是______.(填序号)
①CD=![]() AB;②DE=DF;③S△DEF=2S△CEF;④S△DEF-S△CEF=S△ABC.
AB;②DE=DF;③S△DEF=2S△CEF;④S△DEF-S△CEF=S△ABC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com