
【题目】如图,抛物线y=﹣(x+1)(x﹣3)与x轴分别交于点A、B(点A在B的右侧),与y轴交于点C,⊙P是△ABC的外接圆.
(1)直接写出点A、B、C的坐标及抛物线的对称轴;
(2)求⊙P的半径;
(3)点D在抛物线的对称轴上,且∠BDC>90°,求点D纵坐标的取值范围;
(4)E是线段CO上的一个动点,将线段AE绕点A逆时针旋转45°得线段AF,求线段OF的最小值.
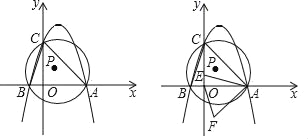
【答案】(1)点B的坐标为(﹣1,0),点A的坐标为(3,0),点C的坐标为(0,3);抛物线的对称轴为直线x=1;(2)⊙P的半径为![]() ;(3)1<y<2;(4)3﹣
;(3)1<y<2;(4)3﹣![]() .
.
【解析】
(1)分别代入y=0、x=0求出与之对应的x、y的值,进而可得出点A、B、C的坐标,再由二次函数的对称性可找出抛物线的对称轴;
(2)连接CP、BP,在Rt△BOC中利用勾股定理可求出BC的长,由等腰直角三角形的性质及圆周角定理可得出∠BPC=90°,再利用等腰直角三角形的性质可求出BP的值即可;
(3)设点D的坐标为(1,y),当∠BDC=90°时,利用勾股定理可求出y值,进而可得出:当1<y<2时,∠BDC>90°;
(4)将△ACO绕点A逆时针方向旋转45°,点C落在点C′处,点O落在点O′处,根据旋转的性质可找出点C′的坐标及∠AC′O′=45°,进而可找出线段C′O′所在直线的解析式,由点E在CO上可得出点F在C′O′上,过点O作OF⊥C′O′于点F,则△OC′F为等腰直角三角形,此时线段OF取最小值,利用等腰直角三角形的性质即可求出此时OF的长即可.
(1)当y=0时,﹣(x+1)(x﹣3)=0,
解得:x1=﹣1,x2=3,
∴点B的坐标为(﹣1,0),点A的坐标为(3,0);
当x=0时,y=﹣(0+1)×(0﹣3)=3,
∴点C的坐标为(0,3);
∵抛物线与x轴交于点(﹣1,0)、(3,0),
∴抛物线的对称轴为直线x=1;
(2)连接CP、BP,如图1所示,
在Rt△BOC中,BC=![]() ,
,
∵∠AOC=90°,OA=OC=3,
∴∠OAC=∠OCA=45°,
∴∠BPC=2∠OAC=90°,
∴CP=BP=![]() BC=
BC=![]() ,
,
∴⊙P的半径为![]() ;
;
(3)设点D的坐标为(1,y),当∠BDC=90°时,BD2+CD2=BC2,
∴[(﹣1﹣1)2+(0﹣y)2]+[(0﹣1)2+(3﹣y)2]=10,
整理,得:y2﹣3y+2=0,
解得:y1=1,y2=2,
∴当1<y<2时,∠BDC>90°;
(4)将△ACO绕点A逆时针方向旋转45°,点C落在点C′处,点O落在点O′处,如图2所示.
∵AC=![]() ,∠ACO=45°,
,∠ACO=45°,
∴点C′的坐标为(3﹣3![]() ,0),∠AC′O′=45°,
,0),∠AC′O′=45°,
∴线段C′O′所在直线的解析式为y=﹣x+3﹣3![]() ,
,
∵点E在线段CO上,
∴点F在线段C′O′上.
过点O作OF⊥C′O′于点F,则△OC′F为等腰直角三角形,此时线段OF取最小值,
∵△OC′F为等腰直角三角形,
∴OF=![]() OC′=
OC′=![]() (3
(3![]() ﹣3)=3﹣
﹣3)=3﹣![]() .
.


科目:初中数学 来源: 题型:
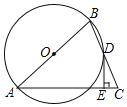
【题目】如图,在![]() 中,
中,![]() ,点D在BC上,
,点D在BC上,![]() ,过点D作
,过点D作![]() ,垂足为E,
,垂足为E,![]() 经过A,B,D三点.
经过A,B,D三点.
![]() 求证:AB是
求证:AB是![]() 的直径;
的直径;
![]() 判断DE与
判断DE与![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
![]() 若
若![]() 的半径为10m,
的半径为10m,![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系xOy中,如果将点P绕点T(0,t)(t>0)旋转180°得到点Q,那么称线段QP为“拓展带”,点Q为点P的“拓展点”.
(1)当t=3时,点(0,0)的“拓展点”坐标为 ,点(﹣1,1)的“拓展点”坐标为 ;
(2)如果 t>1,当点M(2,1)的“拓展点”N在函数y=﹣![]() 的图象上时,求t的值;
的图象上时,求t的值;
(3)当t=1时,点Q为点P(2,0)的“拓展点”,如果抛物线 y=(x﹣m)2﹣1与“拓展带”PQ有交点,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
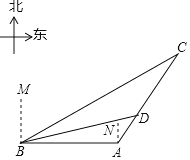
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
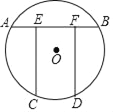
【题目】如图,为一圆洞门.工匠在建造过程中需要一根横梁AB和两根对称的立柱CE、DF来支撑,点A、B、C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AB=2![]() ,EF=
,EF=![]() ,
,![]() =120°.
=120°.
(1)求出圆洞门⊙O的半径;
(2)求立柱CE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
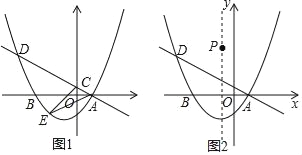
【题目】如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣![]() 与x轴交于点A(1,0)和点B(﹣3,0).绕点A旋转的直线l:y=kx+b1交抛物线于另一点D,交y轴于点C.
与x轴交于点A(1,0)和点B(﹣3,0).绕点A旋转的直线l:y=kx+b1交抛物线于另一点D,交y轴于点C.
(1)求抛物线的函数表达式;
(2)当点D在第二象限且满足CD=5AC时,求直线l的解析式;
(3)在(2)的条件下,点E为直线l下方抛物线上的一点,直接写出△ACE面积的最大值;
(4)如图2,在抛物线的对称轴上有一点P,其纵坐标为4,点Q在抛物线上,当直线l与y轴的交点C位于y轴负半轴时,是否存在以点A,D,P,Q为顶点的平行四边形?若存在,请直接写出点D的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=60°,BC=3厘米,AC=4厘米,点P从点B出发,沿B→C→A以每秒1厘米的速度匀速运动到点A.设点P的运动时间为x秒,B、P两点间的距离为y厘米.

小新根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小新的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x(s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
y(cm) | 0 | 1.0 | 2.0 | 3.0 | 2.7 | 2.7 | m | 3.6 |
经测量m的值是(保留一位小数).
(2)建立平面直角坐标系,描出表格中所有各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:在曲线部分的最低点时,在△ABC中画出点P所在的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com